
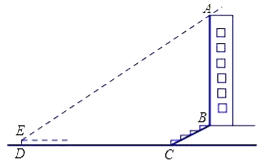
【题目】某校兴趣小组想测量一座大楼AB的高度.如图6,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:![]() .在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)
.在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73.)
≈1.73.)
【答案】33.3.
【解析】
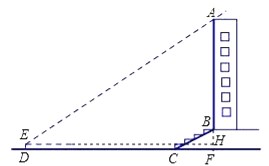
试题分析:延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H,在Rt△BCF中利用坡度的定义求得CF的长,则DF即可求得,然后在直角△AEH中利用三角函数求得AF的长,进而求得AB的长.
试题解析:延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H.
∵在Rt△BCF中,![]() =i=1:
=i=1:![]() ,∴设BF=k,则CF=
,∴设BF=k,则CF=![]() k,BC=2k.
k,BC=2k.
又∵BC=12,∴k=6,∴BF=6,CF=![]() .∵DF=DC+CF,∴DF=40+
.∵DF=DC+CF,∴DF=40+![]() .∵在Rt△AEH中,tan∠AEH=
.∵在Rt△AEH中,tan∠AEH=![]() ,∴AH=tan37°×(40+
,∴AH=tan37°×(40+![]() )≈37.8(米),∵BH=BF﹣FH,∴BH=6﹣1.5=4.5.∵AB=AH﹣HB,∴AB=37.8﹣4.5=33.3.
)≈37.8(米),∵BH=BF﹣FH,∴BH=6﹣1.5=4.5.∵AB=AH﹣HB,∴AB=37.8﹣4.5=33.3.
答:大楼AB的高度约为33.3米.
考点:1.解直角三角形的应用-仰角俯角问题;2.解直角三角形的应用-坡度坡角问题.
【题型】解答题
【结束】
24
【题目】为迎接安顺市文明城市创建工作,某校八年一班开展了“社会主义核心价值观、未成年人基本文明礼仪规范”的知识竞赛活动,成绩分为A、B、C、D四个等级,并将收集的数据绘制了两幅不完整的统计图.请你根据图中所给出的信息,解答下列各题:
(1)求八年一班共有多少人;
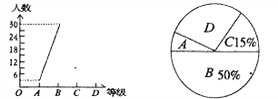
(2)补全折线统计图;
(3)在扇形统计图中等极为“D”的部分所占圆心角的度数为________;
(4)若等级A为优秀,求该班的优秀率.
【答案】(1)60;(2)补图见解析;(3)108°;(4)5%.
【解析】(1)用B等人数除以其所占的百分比即可得到总人数;
(2)用求得的总人数乘以C等所占的百分比即可得到C等的人数,总人数减去A、C等的人数即可求得D等的人数;
(3)用D等的人数除以总人数乘以360°即可得到答案;
(4)用A等的人数除以总人数乘以100%即可得到答案. 解答:
解:(1)30÷50%=60(人)
∴八年级一共有60人。
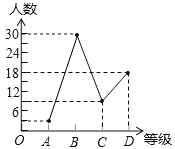
(2)等级为“C”的人数为60×15%=9(人).
等级为“D”的人数为603309=18(人).
补全折线统计图如下。
(3)等极为“D”的部分所占圆心角的度数为![]() ×360°=108°,
×360°=108°,
故答案为:108°.
(4)该班的优秀率![]() ×100%=5%.
×100%=5%.
∴该班的优秀率为5%.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】江西二套“谁是赢家”二七王比赛中,节目要统计 4 位选手的短信支持率,第一次 公布 4 位选手的短信支持率情况如图 1,一段时间后,第二次公布 4 位选手的短信支持率,情况如图 2,第二次公布短信支持率时,每位选手的短信支持条数均有增加, 且每位选手增加的短信支持条数相同.

(1)比较图1,图2的变化情况,写出2条结论;
(2)写出第一次4位短信支持总条数与第二次4位短信支持总条数的等式关系,并证明这个等式关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
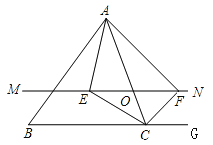
【题目】如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2的正方形ABCD中,AE平分∠DAC,AE交CD于点F,CE⊥AE,垂足为点E,EG⊥CD,垂足为点G,点H在边BC上,BH=DF,连接AH、FH,FH与AC交于点M,以下结论:
①FH=2BH;②AC⊥FH;③S△ACF=1;④CE=![]() AF;⑤
AF;⑤![]() =FGDG,其中正确结论的个数为( )
=FGDG,其中正确结论的个数为( )
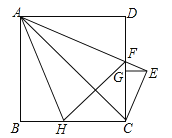
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
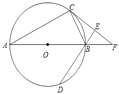
【题目】如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,过点C作CE⊥DB交DB的延长线于点E,直线AB与CE相交于点F.
(1)求证:CF为⊙O的切线;
(2)填空:当∠CAB的度数为________时,四边形ACFD是菱形.
【答案】30°
【解析】(1)连结OC,如图,由于∠A=∠OCA,则根据三角形外角性质得∠BOC=2∠A,而∠ABD=2∠BAC,所以∠ABD=∠BOC,根据平行线的判定得到OC∥BD,再CE⊥BD得到OC⊥CE,然后根据切线的判定定理得CF为⊙O的切线;
(2)根据三角形的内角和得到∠F=30°,根据等腰三角形的性质得到AC=CF,连接AD,根据平行线的性质得到∠DAF=∠F=30°,根据全等三角形的性质得到AD=AC,由菱形的判定定理即可得到结论.
答:
(1)证明:连结OC,如图,
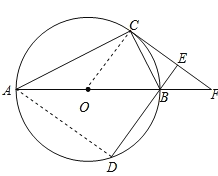
∵OA=OC,
∴∠A=∠OCA,
∴∠BOC=∠A+∠OCA=2∠A,
∵∠ABD=2∠BAC,
∴∠ABD=∠BOC,
∴OC∥BD,
∵CE⊥BD,
∴OC⊥CE,
∴CF为⊙O的切线;
(2)当∠CAB的度数为30°时,四边形ACFD是菱形,理由如下:
∵∠A=30°,
∴∠COF=60°,
∴∠F=30°,
∴∠A=∠F,
∴AC=CF,
连接AD,
∵AB是⊙O的直径,
∴AD⊥BD,
∴AD∥CF,
∴∠DAF=∠F=30°,
在△ACB与△ADB中,
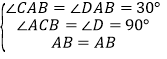 ,
,
∴△ACB≌△ADB,
∴AD=AC,
∴AD=CF,
∵AD∥CF,
∴四边形ACFD是菱形。
故答案为:30°.
【题型】解答题
【结束】
22
【题目】经市场调查,某种商品在第x天的售价与销量的相关信息如下表;已知该商品的进价为每件30元,设销售该商品每天的利润为y元.

(1)求出y与x的函数关系式
(2)问销售该商品第几天时,当天销售利润最大?最大利润是多少?
(3)该商品销售过程中,共有多少天日销售利润不低于4800元?直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为(a,0),点C的坐标为(0,b),且a、b满足![]() +|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
+|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
(1)a=______________,b=_____________,点B的坐标为_______________;
(2)当点P移动4秒时,请指出点P的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC和△DEF是两个边长都为8cm的等边三角形,且 B、D、C、F都在同一条直线上,连接AD、CE
(1)求证:四边形ADEC是平行四边形
(2)若BD=3cm, △ABC沿着BF的方向以每秒1cm的速度运动,设△ABC运动时间为t秒
①当t等于多少秒时,四边形ADEC为菱形;
②点B运动过程中,四边形ADEC有可能是矩形吗?若可能,请画出图形,并求出t的值;若不可能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某加工厂为赶制一批零件,通过提高加工费标准的方式调动工人积极性.工人每天加工零件获得的加工费y(元)与加工个数x(个)之间的部分函数图象为折线OA-AB-BC,如图所示.
(1)求工人一天加工零件不超过20个时每个零件的加工费.
(2)求40≤![]() ≤60时y与x的函数关系式.
≤60时y与x的函数关系式.
(3)小王两天一共加工了60个零件,共得到加工费220元.在这两天中,小王第一天加工零件不足20个,求小王第一天加工的零件个数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com