
����Ŀ���������ס�˭��Ӯ�ҡ������������У���ĿҪͳ�� 4 λѡ�ֵĶ���֧���ʣ���һ�� ���� 4 λѡ�ֵĶ���֧���������ͼ 1��һ��ʱ��ڶ��ι��� 4 λѡ�ֵĶ���֧���ʣ������ͼ 2���ڶ��ι�������֧����ʱ��ÿλѡ�ֵĶ���֧�������������ӣ� ��ÿλѡ�����ӵĶ���֧��������ͬ��

��1���Ƚ�ͼ1��ͼ2�ı仯�����д��2�����ۣ�
��2��д����һ��4λ����֧����������ڶ���4λ����֧���������ĵ�ʽ��ϵ����֤�������ʽ��ϵ��
���𰸡���1���ٶ���֧���ʸ���25%�Ļ��½����ڶ���֧���ʵ���25%�Ļ�䣻��2��b=2a,֤����������
��������
��1����ͼ�еó�3��֧�����½���2��4�ŵ�������1�ŵIJ��䣻
��2�������д�֮����4λѡ�ֵĶ���֧��������ͬ����25%b-25%a=22.5%b-20%a=30%b-35%a�����ɣ�
��1������֮����4λѡ�ֵĶ���֧��������ͬ����£��Ƚ�ͼ1��ͼ2�ı仯�������֪��
�ٶ���֧���ʸ���25%�Ļ��½���
�ڶ���֧���ʵ���25%�Ļ�䣻
�۶���֧���ʵ���25%�Ļ�������
��2�����һ��4λ����֧��������Ϊa��ڶ���4λ����֧��������b�����ǵ�ʽ��ϵΪ��b=2a��
֤�����£�
������֮����4λѡ�ֵĶ���֧��������ͬ
��25%b-25%a=22.5%b-20%a=30%b-35%a
�����ã�b=2a��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ĸ���˿���������������ı���Χ��һ��ľ����״���ޣ���������˿��С��������������˿֮��ľ�������Ϊ3��4��5��7.�������������ļнǾ��ɵ�����������ľ���ļн�ʱ���ƻ���ľ��������������˿֮����������ǣ� ��
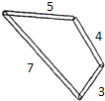
A.6B.7C.8D.9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
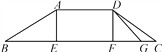
����Ŀ��Ϊ�˷������ˣ���������������ͼ��ʾ�Ĺ������ţ�����ADƽ���ڵ���BC������AE��BC�ڵ�E������DF��BC�ڵ�F����AB��5![]() �ף�tanB��
�ף�tanB��![]() ����C��30��.
����C��30��.
(1)������AD�����BC֮��ľ��룮
(2)���ܵ������ƣ������Ը����Ž��иĽ���ʹCDб����¶ȱ䶸������30���½Ǹ�Ϊ40�����Ľ���б��ΪDG���Լ���˴θĽ���ʡ·�����CG��ԼӦ�Ƕ��٣�(�����ȷ��0.1�ף��ο����ݣ�sin40���0.64��cos40���0.77��tan40���0.84��![]() ��1.732)
��1.732)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����C��AOB��һ��OA�ϣ�����C��ֱ��DE//OB��CFƽ��ACD��CG CF��C ��
��1����O =40����ECF�Ķ�����
��2����֤��CGƽ��OCD��
��3����OΪ���ٶ�ʱ��CDƽ��OCF����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ѧ��������ʶ���ؿ�ѧ����Ұ���ٽ�ѧϰ�����������ں�����ij��ѧ������֯����ѧ��ȥ�������ۺ�ʵ�����ؽ����ۺ�ʵ����ڲμӴ˴λ��ʦ���У���ÿλ��ʦ��17��ѧ������ʣ12��ѧ��û�˴�����ÿλ��ʦ��18��ѧ��������һλ��ʦ�ٴ�4��ѧ�����мס������ִ�ͳ����ǵ��ؿ�������������ʾ
���ֿͳ� | ���ֿͳ� | |
�ؿ�������/���� | 30 | 42 |
���Ԫ/���� | 300 | 400 |
ѧУ�ƻ���ʵ�������ܷ��ò�����3100Ԫ��Ϊ�˰�ȫÿ���ͳ�������Ҫ��2����ʦ��
��1���μӴ˴��ۺ�ʵ�������ʦ��ѧ�����ж����ˣ�
��2����Ҫ��֤����ʦ�����г�������Ҫ��֤ÿ���ͳ�������Ҫ��2����ʦ�����ÿͳ�����Ϊ��������
��3�����ܵó��ļ��ֲ�ͬ������������������������ʡǮ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABCD������AB��AD�ij��ǹ���x�ķ���x2��mx��![]() ��
��![]() ��0������ʵ������
��0������ʵ������
(1)��mΪ��ֵʱ���ı���ABCD�����Σ������ʱ���εı߳���
(2)��AB�ij�Ϊ2����ô��ABCD���ܳ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�Ƶ�A˳ʱ����ת������AB��C��D����λ�ã���ת��Ϊ����0��������90����������1=110�������Ϧ�= ��
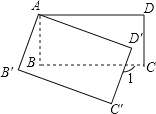
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABCD�У�EF���Խ��ߵĽ��㣬��AB��4��BC��7��OE��1.5�����ı���EFDC���ܳ��ǣ� ��

A. 14B. 17C. 10D. 11
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��ȤС�������һ����¥AB�ĸ߶ȣ���ͼ6����¥ǰ��һ��б��BC����֪BC�ij�Ϊ12�ף������¶�i=1��![]() ������C��40��D�����ò���Dz�ô�¥����A������Ϊ37�㣬�����DE�ĸ�Ϊ1.5�ף����¥AB�ĸ߶�ԼΪ�����ף��������ȷ��0.1�ף�
������C��40��D�����ò���Dz�ô�¥����A������Ϊ37�㣬�����DE�ĸ�Ϊ1.5�ף����¥AB�ĸ߶�ԼΪ�����ף��������ȷ��0.1�ף�
���ο����ݣ�sin37����0.60��cos37����0.80��tan37����0.75��![]() ��1.73����
��1.73����
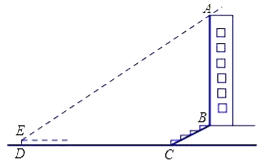
���𰸡�33.3��
��������
����������ӳ�AB��ֱ��DC�ڵ�F������E��EH��AF������Ϊ��H����Rt��BCF�������¶ȵĶ������CF�ij�����DF������ã�Ȼ����ֱ����AEH���������Ǻ������AF�ij����������AB�ij���
����������ӳ�AB��ֱ��DC�ڵ�F������E��EH��AF������Ϊ��H��
����Rt��BCF��![]() =i=1��
=i=1��![]() ������BF=k����CF=
������BF=k����CF=![]() k��BC=2k��
k��BC=2k��
����BC=12����k=6����BF=6��CF=![]() ����DF=DC+CF����DF=40+
����DF=DC+CF����DF=40+![]() ������Rt��AEH��tan��AEH=
������Rt��AEH��tan��AEH=![]() ����AH=tan37������40+
����AH=tan37������40+![]() ����37.8���ף�����BH=BF��FH����BH=6��1.5=4.5����AB=AH��HB����AB=37.8��4.5=33.3��
����37.8���ף�����BH=BF��FH����BH=6��1.5=4.5����AB=AH��HB����AB=37.8��4.5=33.3��
�𣺴�¥AB�ĸ߶�ԼΪ33.3�ף�
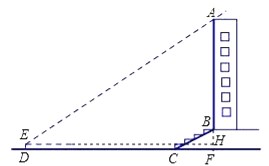
���㣺1����ֱ�������ε�Ӧ��-���Ǹ������⣻2����ֱ�������ε�Ӧ��-�¶��½����⣮
�����͡������
��������
24
����Ŀ��Ϊӭ�Ӱ�˳���������д���������ijУ����һ�չ�ˡ����������ļ�ֵ�ۡ�δ�����˻����������ǹ淶����֪ʶ��������ɼ���ΪA��B��C��D�ĸ��ȼ��������ռ������ݻ�����������������ͳ��ͼ.�������ͼ������������Ϣ��������и���:
(1)�����һ��ж����ˣ�
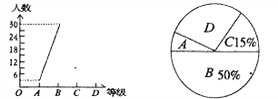
(2)��ȫ����ͳ��ͼ��
(3)������ͳ��ͼ�еȼ�Ϊ��D���IJ�����ռԲ�ĽǵĶ���Ϊ________��
(4)���ȼ�AΪ���㣬��ð��������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com