练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在□ABCD中，EF过对角线的交点，若AB＝4，BC＝7，OE＝1.5，则四边形EFDC的周长是（ ）

    A. 14B. 17C. 10D. 11

    【答案】A

    【解析】

    由在平行四边形ABCD中，EF过两条对角线的交点O，易证得△AOE≌△COF，则可得DE+CF=AD，EF=2OE=6，继而求得四边形EFCD的周长．

    ∵四边形ABCD是平行四边形，
    ∴AD∥BC，OA=OC，CD=AB=4，AD=BC=7
    ∴∠EAO=∠FCO，
    在△AOE和△COF中，

    ，
    ∴△AOE≌△COF（ASA），
    ∴AE=CF，OE=OF=1.5，
    ∴EF=3，
    ∴四边形EFCD的周长是：CD+DE+EF+CF=CD+DE+AE+EF=CD+AD+EF=4+7+3=14．
    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

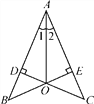
    【题目】如图，已知CD⊥AB，BE⊥AC，垂足分别为点D，点E，BE，CD相交于点O，连接AO.求证：

    (1)当∠1＝∠2时，OB＝OC；

    (2)当OB＝OC时，∠1＝∠2.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】江西二套“谁是赢家”二七王比赛中，节目要统计 4 位选手的短信支持率，第一次 公布 4 位选手的短信支持率情况如图 1，一段时间后，第二次公布 4 位选手的短信支持率，情况如图 2，第二次公布短信支持率时，每位选手的短信支持条数均有增加， 且每位选手增加的短信支持条数相同．

    （1）比较图1，图2的变化情况，写出2条结论；

    （2）写出第一次4位短信支持总条数与第二次4位短信支持总条数的等式关系，并证明这个等式关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算或解方程：

    (1)

    (2)

    (3) 解方程:

    (4) 解方程:

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了抓住梵净山文化艺术节的商机，某商店决定购进A、B两种艺术节纪念品．若购进A种纪念品8件，B种纪念品3件，需要950元；若购进A种纪念品5件，B种纪念品6件，需要800元．

    （1）求购进A、B两种纪念品每件各需多少元？

    （2）若该商店决定购进这两种纪念品共100件，考虑市场需求和资金周转，用于购买这100件纪念品的资金不少于7500元，但不超过7650元，那么该商店共有几种进货方案？

    （3）若销售每件A种纪念品可获利润20元，每件B种纪念品可获利润30元，在第（2）问的各种进货方案中，哪一种方案获利最大？最大利润是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图(1)，AB为半圆O的直径，D为BA的延长线上一点，DC为半圆O的切线，切点为C．

    （1）求证：∠ACD=∠B；

    （2）如图(2)，∠BDC的平分线分别交AC，BC于点E，F，求∠CEF的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

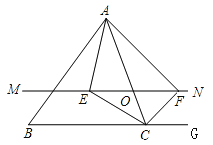
    【题目】如图，在△ABC中，点O是AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的角平分线于点E，交∠BCA的外角平分线于点F．

    （1）求证：EO=FO；

    （2）当点O运动到何处时，四边形AECF是矩形？并证明你的结论．

    （3）当点O运动到何处，且△ABC满足什么条件时，四边形AECF是正方形？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，边长为2的正方形ABCD中，AE平分∠DAC，AE交CD于点F，CE⊥AE，垂足为点E，EG⊥CD，垂足为点G，点H在边BC上，BH=DF，连接AH、FH，FH与AC交于点M，以下结论：

    ①FH=2BH；②AC⊥FH；③S△ACF=1；④CE=AF；⑤=FGDG，其中正确结论的个数为（　　）

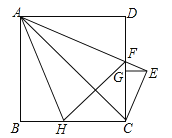
    A. 2 B. 3 C. 4 D. 5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC和△DEF是两个边长都为8cm的等边三角形，且 B、D、C、F都在同一条直线上，连接AD、CE

    （1）求证：四边形ADEC是平行四边形

    （2）若BD=3cm, △ABC沿着BF的方向以每秒1cm的速度运动，设△ABC运动时间为t秒

    ①当t等于多少秒时，四边形ADEC为菱形；

    ②点B运动过程中，四边形ADEC有可能是矩形吗？若可能，请画出图形，并求出t的值；若不可能，请说明理由.

    查看答案和解析>>

    同步练习册答案