
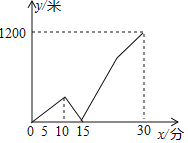
����Ŀ��һ���糿��С��Ӽҳ������ٲ��е�ѧУ��С�����һ��ʱ����������跢��С��������һ�������ѧϰ��Ʒ������������¥�����г�����С���н���·�ߣ�����ȥС�ᣬ������С�Ὣѧϰ��Ʒ����С���������ԭ·�����ٷ��ؼ��������·�����˽��࣬���践��ʱ�ﳵ���ٶ�ֻ��ԭ���ٶȵ�һ�룬С�������ԭ�ٶȲ���ǰ��ѧУ��������С��֮��ľ���y���ף���С��Ӽҳ������е�ʱ��x���֣�֮��Ĺ�ϵ��ͼ��ʾ��С��������ϡ���¥�Լ����轻ѧϰ��Ʒ��С�ᵢ���ʱ����Բ��ƣ���������ջص���ʱ��С����ѧУ�ľ���Ϊ_____�ף�
���𰸡�200
��������
��ͼ���֪���ҵ�ѧУ��·��Ϊ1200�ף��ֱ���С���������ٶȣ����践��ʱ�����������践��ʱ�ﳵ���ٶ�ֻ��ԭ���ٶȵ�һ���������ٶ�Ϊ60��/�֣��ɵ÷���ʱ������10���ӣ���ʱС���Ѿ�����25�֣���ʣ5���ӵ��̣ܳ�
��ͼ��ã�С�Ჽ���ٶȣ�1200��30=40����/�֣���
�ɺ���ͼ��ó���������С��10�ֺ������15��ʱ��С�ᣬ
������ȥʱ���ٶ�Ϊv��/�֣�
��15-10��v=15��40��
v=120��
������ؼҵ�ʱ�䣺![]() =10��
=10��
��30-15-10����40=200��
�ʴ�Ϊ200��


 ����Ӣ��ϵ�д�
����Ӣ��ϵ�д� ����ѧУ�ֲ����ܲ�ϵ�д�
����ѧУ�ֲ����ܲ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
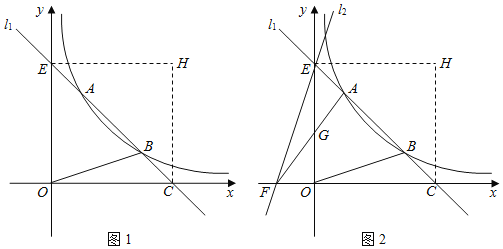
����Ŀ����ͼ1��ֱ��![]() ��˫����
��˫����![]() ����
����![]() ��
��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ����֪��
����֪��![]() ����
����![]() ��
��
��1����ֱ��![]() ��˫���ߵĽ���ʽ��
��˫���ߵĽ���ʽ��
��2����![]() ��ֱ��
��ֱ��![]() ���ۣ���
���ۣ���![]() ���ڵ�һ�����ڵĵ�
���ڵ�һ�����ڵĵ�![]() ����ֱ��д����
����ֱ��д����![]() �����ꣻ
�����ꣻ
��3����ͼ2������![]() ��ֱ��
��ֱ��![]() ��
��![]() ��ĸ������ڵ�
��ĸ������ڵ�![]() ������
������![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() �������
�������![]() �������ȣ�
�������ȣ�
����ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
����ֱ��![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() �������ڣ���ֱ��д�����з��������ĵ�
�������ڣ���ֱ��д�����з��������ĵ�![]() �����ꣻ��������ڣ���˵�����ɣ�
�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ʽx3��3xy2��3�ij�������a��������b����a=������������b=������������
��������������ͼ��ʾ����������Ӧ�ĵ�A��B��ʾ������
![]()
����̽����
����һ��
(1)�۵�ֽ��,ʹA��ʾ�ĵ���B��ʾ�ĵ��غϣ���5��ʾ�ĵ���__ ___��ʾ�ĵ��غϣ�
�������� (2)�۵�ֽ��,ʹ1��ʾ�ĵ���3��ʾ�ĵ��غϣ��ش��������⣺
��![]() ��ʾ�ĵ�����_____��ʾ�ĵ��غϣ�
��ʾ�ĵ�����_____��ʾ�ĵ��غϣ�
����������C��D����֮�����Ϊ9��(C��D�����)����C��D���㾭�۵����غ�,��C��D�����ʾ�����Ƕ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ĸ�������a��b��c��d���������������������(a��b)��(c��d)�����ǹ涨(a��b)��(c��d)=bc-ad
����:(1��2)��(3��4)=2��3-1��4=2
���������涨����������⣺
��1����������(4��-3)��(3��-2)=_______
��2������������(-3��2x-1)��(1��x+1)=7����x=______
��3���������ʽ(-3��2x-1)��(k��x+k)=5+2k��x�Ƿ�������ʱ��������k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ͺ�������������Ϊ40L��ÿ��ʻ100km����10L.��һ�������͵ĸ��ͺ�������ʻ·��Ϊx��km������ʻ������������ʣ������Ϊy��L��
��1����y��x֮��ĺ�������ʽ��
��2��Ϊ����Ч�ӳ�����ʹ�����������ҽ���ÿ�μ���ʱ������ʣ�����������������������ķ�֮һ�����˽��飬��������������ʻ��·��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪DΪ��ABC��BC�ߵ��е㣬DE��DF�ֱ�ƽ�֡�ADB�͡�ADC��
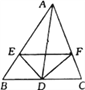
��֤��BE��CF>EF.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�й涨��ÿ����ˮ18���������ڣ���18�����ף�����ˮ18�������������ֲ�ͬ���շѱ������е��û�ÿ��Ӧ��ˮ��y��Ԫ������ˮ��x�������ף��ĺ�������ͼ����ͼ��ʾ��
��1����ij����ˮ��Ϊ18�����ף���Ӧ��ˮ�Ѷ���Ԫ��
��2����x��18ʱ��y����x�ĺ�������ʽ����С����ij�½�ˮ��81Ԫ�����������ˮ��Ϊ���������ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��C����ֱ��l����AE��AB��AE=AB��BC��CD��BC=CD������E��B��D��ֱ��l�ľ���ֱ���6��3��4������ͼ�����߶�AB��BC��CD��DE��EA��Χ�ɵ�ͼ�ε��������������
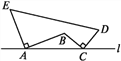
A. 50 B. 62 C. 65 D. 68
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
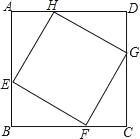
����Ŀ����ͼ����������ABCD�У���E��F��G��H�ֱ���AB��BC��CD��DA���ϵĶ��㣬��AE=BF=CG=DH��
��1����֤����AEH�ա�CGF��
��2���ڵ�E��F��G��H�˶������У��ж�ֱ��EG�Ƿ�ijһ�����㣬����ǣ���֤����Ľ��ۣ�������ǣ���˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com