
【题目】如图,已知D为△ABC的BC边的中点,DE、DF分别平分∠ADB和∠ADC,
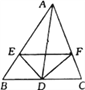
求证:BE+CF>EF.
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两同学在一次百米赛跑中,路程S(米)与时间t(秒)之间的关系如图所示.根据图象回答下列问题:

(1)3.8秒时,哪位同学处于领先位置?
(2)在这次赛跑中,哪位同学先到达终点?比另一个同学早多少时间到达?约几秒后哪位同学被哪位同学追上?
(3)甲同学所走的路程S(米)与时间t(秒)之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
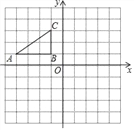
【题目】如图,在平面直角坐标系中,Rt△ABC三个顶点都在格点上,点A、B、C的坐标分别为A(﹣4,1),B(﹣1,1),C(﹣1,3)请解答下列问题:
(1)画出△ABC关于原点O的中心对称图形△A1B1C1,并写出点C的对应点C1的坐标;
(2)画出△ABC绕原点O逆时针旋转90°后得到的△A2B2C2,并直接写出点A旋转至A2经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
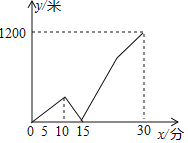
【题目】一天早晨,小玲从家出发匀速步行到学校,小玲出发一段时间后,她的妈妈发现小玲忘带了一件必需的学习用品,于是立即下楼骑自行车,沿小玲行进的路线,匀速去追小玲,妈妈追上小玲将学习用品交给小玲后,立即沿原路线匀速返回家里,但由于路上行人渐多,妈妈返回时骑车的速度只是原来速度的一半,小玲继续以原速度步行前往学校,妈妈与小玲之间的距离y(米)与小玲从家出发后步行的时间x(分)之间的关系如图所示(小玲和妈妈上、下楼以及妈妈交学习用品给小玲耽搁的时间忽略不计).当妈妈刚回到家时,小玲离学校的距离为_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
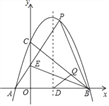
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),B(4,0),与y轴交于点C(0,4).
(1)求此抛物线的解析式;
(2)设点P(2,n)在此抛物线上,AP交y轴于点E,连接BE,BP,请判断△BEP的形状,并说明理由;
(3)设抛物线的对称轴交x轴于点D,在线段BC上是否存在点Q,使得△DBQ成为等腰直角三角形?若存在,求出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数的图象经过点A(2,1),B(﹣1,﹣3).
(1)求此一次函数的解析式;
(2)求此一次函数的图象与x轴、y轴的交点坐标;
(3)求此一次函数的图象与两坐标轴所围成的三角形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD
(1)求证:BE=AD;
(2)求证:AC是线段ED的垂直平分线;
(3)△DBC是等腰三角形吗?并说明理由

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=![]() (x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(1)求反比例函数和直线EF的解析式;
(2)求△OEF的面积;
(3)请结合图象直接写出不等式k2x+b﹣![]() >0的解集.
>0的解集.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com