
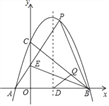
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),B(4,0),与y轴交于点C(0,4).
(1)求此抛物线的解析式;
(2)设点P(2,n)在此抛物线上,AP交y轴于点E,连接BE,BP,请判断△BEP的形状,并说明理由;
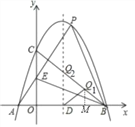
(3)设抛物线的对称轴交x轴于点D,在线段BC上是否存在点Q,使得△DBQ成为等腰直角三角形?若存在,求出点Q的坐标;若不存在,说明理由.
【答案】(1)y=﹣x2+3x+4;(2)△BEP为等腰直角三角形,理由见解析;(3)存在,Q的坐标为![]() 或
或![]() .
.
【解析】试题分析:(1)待定系数法求二次函数解析式.(2)先求出直线AP解析式,分别求出BE,EP,BP的长度,由勾股定理逆定理△BEP的形状.(3)先求出二次函数的顶点,分类讨论,若BQ=DQ,BQ1⊥DQ1,∠BDQ=45°,过点Q1作Q1M⊥OB,垂足为M,可求得△DBQ是等腰三角形,可以得到Q点,若DQ2=BD,DQ2⊥BD,可以计算出Q点.
试题解析:
解:(1)∵抛物线上A、B、C三点坐标代入抛物线解析式y=ax2+bx+c
得,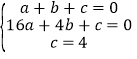 ,
,
解得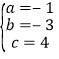 ,
,
∴抛物线的解析式为y=﹣x2+3x+4.
(2)结论:△BEP为等腰直角三角形,理由如下:
∵点P(2,n)在此抛物线上,
∴n=﹣4+6+4=6,
∴P点坐标为(2,6).
设直线AP解析式为y=kx+b,
把A、P两点坐标代入可得![]() ,
,
解得![]() ,
,
∴直线AP的解析式为y=2x+2,
令x=0可得y=2,则E点坐标为(0,2).
∵B(4,0),P(2,6),
∴BP=2![]() ,BE=2
,BE=2![]() ,EP=2
,EP=2![]()
∴BE2+EP2=20+20=40=BP2,且BE=EP,
∴△BEP为等腰直角三角形.
(3)存在.
∵y=﹣x2+3x+4=﹣(x﹣![]() )2+
)2+![]() ,
,
∴顶点的坐标为(![]() ,
,![]() ),
),
∵OB=OC=4,∴BC=4![]() ,∠ABC=45°.
,∠ABC=45°.
以下分两种情况:
①若BQ=DQ,BQ1⊥DQ1,∠BDQ=45°,如图,过点Q1作Q1M⊥OB,垂足为M,
∵BQ1=DQ1,BD=4﹣![]() =
=![]() ,
,
∴BM=Q1M=![]() ,OM=4﹣
,OM=4﹣![]() =
=![]() ,
,
∴Q1的坐标为Q1(![]() ,
,![]() ).
).
②若DQ2=BD=![]() ,DQ2⊥BD,易得BC所在的直线解析式为y=﹣x+4,
,DQ2⊥BD,易得BC所在的直线解析式为y=﹣x+4,
代入x=![]() ,得y=﹣
,得y=﹣![]() +4=
+4=![]() ,
,
∴DQ2=BD=![]() ,∴△BDQ2是等腰直角三角形,
,∴△BDQ2是等腰直角三角形,
所以Q2的坐标为Q2(![]() ,
,![]() ),
),
综上所述,Q的坐标为Q1(![]() ,
,![]() )或Q2(
)或Q2(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】用棋子摆成如图所示的“T”字图案.

(1)摆成第一个“T”字需要多少枚棋子,第二个呢?按这样的规律摆下去,摆成第10个“T”字需要多少枚个棋子?
(2)第![]() 个需多少枚棋子?
个需多少枚棋子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学库存若干套桌椅,准备修理后支援贫困山区学校.现有甲、乙两个木工组,甲组每天修理桌椅16套,乙组每天修理桌椅比甲组多8套.甲组单独修理完这些桌椅比乙组单独修理完多用20天.学校每天付甲组80元修理费,付乙组120元修理费.
(1)该中学库存多少套桌椅?
(2)在修理过程中,学校要派一名工人进行质量监督,学校负担他每天20元生活补助费.现有三种修理方案:
方案一,由甲组单独修理;
方案二,由乙组单独修理;
方案三,甲、乙两组同时修理.
你认为哪种方案省时又省钱?为什么.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+4的图象与反比例函数y=![]() (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,根据材料回答:
例如1:![]()
![]()
![]()
![]()
![]() .
.
例如2:
8![]() ×0.125
×0.125![]() =8×8×8×8×8×8×0.125×0.125×0.125×0.125×0.125×0.125
=8×8×8×8×8×8×0.125×0.125×0.125×0.125×0.125×0.125
=(8×0.125)×(8×0.125)×(8×0.125)×(8×0.125)×(8×0.125)×(8×0.125)
=(8×0.125)6 =1.
(1)仿照上面材料的计算方法计算:![]() ;
;
(2)由上面的计算可总结出一个规律:(用字母表示) ![]() ;
;
(3)用(2)的规律计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系图象如图所示,根据图中提供的信息,有下列说法:

(1)他们都行驶了18千米;
(2)甲在途中停留了0.5小时;
(3)乙比甲晚出发了0.5小时;
(4)相遇后,甲的速度小于乙的速度;
(5)甲、乙两人同时到达目的地
其中符合图象描述的说法有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】秋季运动会上,七年级(1)班的萌萌、路佳、王玉三人一起进行50米赛跑(假定三人均为匀速直线运动).如果当萌萌到达终点时,路佳距终点还有5米,王玉距终点还有10米.那么当路佳到达终点时,王玉距终点还有________米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com