
【题目】如图,一次函数y=﹣x+4的图象与反比例函数y=![]() (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.

【答案】(1)反比例函数的表达式y=![]() ,点B的坐标为(3,1).(2)
,点B的坐标为(3,1).(2)![]() .
.
【解析】试题分析:(1)由点A在一次函数图象上,结合一次函数解析式可求出点A的坐标,再由点A的坐标利用待定系数法即可求出反比例函数解析式,联立两函数解析式成方程组,解方程组即可求出点B坐标;
(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,连接PB.由点B、D的对称性结合点B的坐标找出点D的坐标,设直线AD的解析式为y=mx+n,结合点A、D的坐标利用待定系数法求出直线AD的解析式,令直线AD的解析式中y=0求出点P的坐标,再通过分割图形结合三角形的面积公式即可得出结论.
试题解析:(1)把点A(1,a)代入一次函数y=-x+4,
得:a=-1+4,解得:a=3,
∴点A的坐标为(1,3).
把点A(1,3)代入反比例函数y=![]() ,
,
得:3=k,
∴反比例函数的表达式y=![]() ,
,
联立两个函数关系式成方程组得: 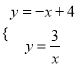 ,
,
解得: ![]() ,或
,或![]() ,
,
∴点B的坐标为(3,1).
(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,此时PA+PB的值最小,连接PB,如图所示.
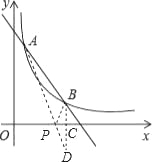
∵点B、D关于x轴对称,点B的坐标为(3,1),
∴点D的坐标为(3,- 1).
设直线AD的解析式为y=mx+n,
把A,D两点代入得: ![]() ,
,
解得: ![]() ,
,
∴直线AD的解析式为y=-2x+5.
令y=-2x+5中y=0,则-2x+5=0,
解得:x=![]() ,
,
∴点P的坐标为(![]() ,0).
,0).
S△PAB=S△ABD-S△PBD=![]() BD(xB-xA)-
BD(xB-xA)-![]() BD(xB-xP)
BD(xB-xP)
=![]() ×[1-(-1)]×(3-1)-
×[1-(-1)]×(3-1)-![]() ×[1-(-1)]×(3-
×[1-(-1)]×(3-![]() )
)
=![]() .
.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】小丽剪了一些直角三角形纸片,她取出其中的几张进行了如下的操作:
操作一:如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
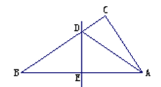
(1)如果AC=6cm,BC=8cm,试求△ACD的周长.
(2)如果∠CAD:∠BAD=4:7,求∠B的度数.
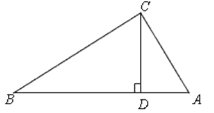
操作二:如图,小丽拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,已知两直角边AC=6cm,BC=8cm,你能求出CD的长吗?
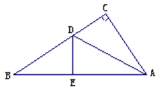
操作三:如图,小丽又拿出另一张Rt△ABC纸片,将纸片折叠,折痕CD⊥AB。你能证明:BC2+AD2=AC2+BD2吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校9月的水费为![]() 元,电费比水费的2倍多40元,10月的水费比9月多支出了25%,电费比9月节约了25%.
元,电费比水费的2倍多40元,10月的水费比9月多支出了25%,电费比9月节约了25%.
(1)用![]() 表示该校9月的电费是多少元?
表示该校9月的电费是多少元?
(2)用![]() 表示该校10月的水、电费各是多少元?
表示该校10月的水、电费各是多少元?
(3)如果该校10月的水、电费共1130元,那么10月的水电费与9月相比超支或节约了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若有![]() 两个数,满足关系式
两个数,满足关系式![]() ,则称
,则称![]() 为“共生数对",记作
为“共生数对",记作![]() .
.
例如:当2, 3满足![]() 时,则(2, 3)是“共生数对".
时,则(2, 3)是“共生数对".
(1)若![]() 是“共生数对",求
是“共生数对",求![]() 的值:
的值:
(2)若![]() 是“共生数对“,判断
是“共生数对“,判断![]() 是否也是“共生数对",请通过计算说明:
是否也是“共生数对",请通过计算说明:
(3)请再写出两个不同的“共生数对”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(-4,0).
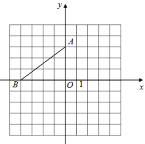
(1)画出△AOB绕点A逆时针旋转90°后得到的图形△A1O1B1;并写出点B1的坐标 ;
(2)画出△AOB关于点P(0,-1)的中心对称图形△A2O2B2,并写出点B2的坐标 ;
(3)若点Q为x轴上的一点,当B1Q+B2 Q的和最小时,直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆格力厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸r的范围为176≤r≤185的产品为合格),随机各抽取了20个样品进行检测,过程如下:
收集数据(单位:mm)
甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183
整理数据
级别 频数 | 165.5~ 170.5 | 170.5~ 175.5 | 175.5~ 180.5 | 180.5~ 185.5 | 185.5 ~190.5 | 190.5~ 195.5 |
甲车间 | 2 | 4 | a | b | 2 | 1 |
乙车间 | 1 | 2 | 9 | 6 | 2 | 0 |
分析数据:
车间 | 平均数 | 众数 | 中位数 | 方差 |
甲车间 | 180 | 185 | 180 | 43.1 |
乙车间 | 180 | 180 | c | 22.6 |
应用数据
(2)请写出表中a= ,b= ,c= mm.
(2)估计甲车间生产的1000个该款新产品中合格产品有多少个?
(3)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
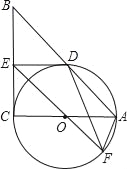
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)若⊙O的半径为3,ED=4,EO的延长线交⊙O于F,连DF、AF,求△ADF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小张某天上午营运全是在东西走向的政府大道上进行的,如果规定向东为正,向西为负,他这天上午的行程是(单位:千米):+15,-3,+16,-11,+10,-12,+4,-15,+16,-18.
(1)将最后一名乘客送达目的地时,小张距上午出发点的距离是多少千米?在出发点的什么方向?
(2)若汽车耗油量为0.6升/千米,出车时,邮箱有油72.2升,若小张将最后一名乘客送达目的地,再返回出发地,问小张今天上午是否需要加油?若要加油至少需要加多少才能返回出发地?若不用加油,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
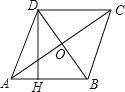
【题目】如图,四边形ABCD是菱形,对角线AC和BD相交于点O,AC=8cm,BD=6cm,DH⊥AB于H.
(1)求菱形ABCD的面积;
(2)求DH的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com