
【题目】小丽剪了一些直角三角形纸片,她取出其中的几张进行了如下的操作:
操作一:如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
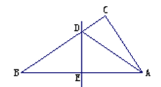
(1)如果AC=6cm,BC=8cm,试求△ACD的周长.
(2)如果∠CAD:∠BAD=4:7,求∠B的度数.
操作二:如图,小丽拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,已知两直角边AC=6cm,BC=8cm,你能求出CD的长吗?
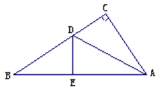
操作三:如图,小丽又拿出另一张Rt△ABC纸片,将纸片折叠,折痕CD⊥AB。你能证明:BC2+AD2=AC2+BD2吗?
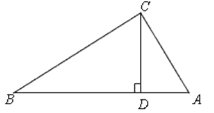
【答案】操作一:(1)14cm;(2)∠B=35°;操作二:CD=3cm;操作三:见解析.
【解析】
操作一 利用对称找准相等的量:BD=AD,∠BAD=∠B,然后分别利用周长及三角形的内角和可求得答案;
操作二 利用折叠找着AC=AE,利用勾股定理列式求出AB,设CD=x,表示出BD,AE,在Rt△BDE中,利用勾股定理可得答案;
操作三 两次运用勾股定理可答案.
解:操作一:
(1)由对称性可得AD=BD,∵△ACD的周长=AC+CD+AD,
∴△ACD的周长=AC+CD+BD=AC+BC=8+6=14(cm);
(2)设∠CAD=4x,∠BAD=7x由题意得方程:7x+7x+4x=90,
解之得x=5,
所以∠B=35°;
操作二:∵AC=6cm,BC=8cm,
∴AB=![]() =10cm,
=10cm,
根据折叠性质可得AC=AE=6cm,
∴BE=AB-AE=10-6=4,
设CD=x,则BD=8-x,DE=x,
在Rt△BDE中,由题意可得方程x2+4=(8-x)2,
解之得x=3,
∴CD=3cm;
操作三:
在Rt△BCD中,由勾股定理可得BC2=BD2+CD2
在Rt△ACD中,由勾股定理可得AD2+CD2=AC2
∴BC2+AD2=BD2+CD2+AD2=AC2+BD2


科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用了随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.

请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 .
(2)请补全条形统计图.
(3)若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用画树状图或列表的方法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
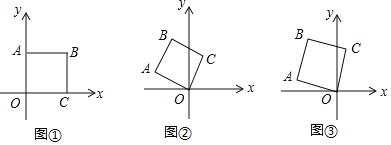
【题目】如图①,将边长为2的正方形OABC如图①放置,O为原点.
(Ⅰ)若将正方形OABC绕点O逆时针旋转60°时,如图②,求点A的坐标;
(Ⅱ)如图③,若将图①中的正方形OABC绕点O逆时针旋转75°时,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
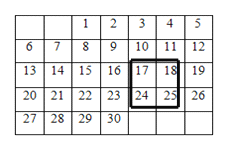
【题目】仔细观察下面的日历,回答下列问题:
(1)任意用正方形框圈出四个日期,如果正方形框中的第一个数(左上角的数)为![]() ,用代数式表示正方形框中的四个数的和;
,用代数式表示正方形框中的四个数的和;
(2)若将正方形框上下左右移动,可框住另外的四个数,这四个数的和能等于![]() 吗?如果能,依次写出这四个数;如果不能,请说明理由.
吗?如果能,依次写出这四个数;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三方面为选手打分,各项成绩均按百分制,进入决赛的两名选手的单项成绩如下表所示:
选手 | 演讲内容 | 演讲能力 | 演讲效果 |
甲 | 85 | 95 | 95 |
乙 | 95 | 85 | 95 |
(1)如果认为这三方面的成绩同等重要,从他们的成绩看,谁能胜出?
(2)如果按演讲内容占50%,演讲能力占40%,演讲效果占10%的比例计算甲、乙的平均成绩,那么谁将胜出?
查看答案和解析>>
科目:初中数学 来源: 题型:
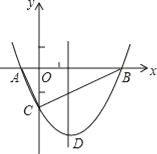
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM周长最小时,求点M的坐标及△ACM的最小周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当∠BAC= 时,矩形AEBD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是小华同学一个学期数学成绩的记录.根据表格提供的信息,回答下列的问题:
考试类别 | 平时考试 | 期中考试 | 期末考试 | |||
第一单元 | 第二单元 | 第三单元 | 第四单元 | |||
成绩(分) | 85 | 78 | 90 | 91 | 90 | 94 |
(1)小明6次成绩的众数是 ,中位数是 ;
(2)求该同学这个同学这一学期平时成绩的平均数;
(3)总评成绩权重规定如下:平时成绩占20%,期中成绩占30%,期末成绩占50%,请计算出小华同学这一个学期的总评成绩是多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+4的图象与反比例函数y=![]() (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com