练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】阅读材料，根据材料回答：

    例如1：

    .

    例如2：

    8×0.125＝8×8×8×8×8×8×0.125×0.125×0.125×0.125×0.125×0.125

    ＝(8×0.125)×(8×0.125)×(8×0.125)×(8×0.125)×(8×0.125)×(8×0.125)

    ＝(8×0.125)6 ＝1.

    （1）仿照上面材料的计算方法计算：；

    （2）由上面的计算可总结出一个规律：(用字母表示) ；

    （3）用（2）的规律计算：.

    【答案】(1)1；（2）；（3）.

    【解析】

    （1）根据同底数幂的乘法法则计算即可求解；
    （2）根据题意找到规律即可；
    （3）逆用积的乘方法则计算即可求解．

    解：（1）=

    =

    =

    =

    =.

    （2）根据题意可得：

    （3）

    =

    =

    =

    ==.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

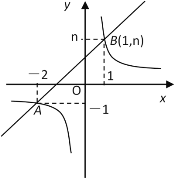
    【题目】如图，一次函数的图象与反比例函数的图象交于A（-2，-1）、B（1，n）两点。

    (1)利用图中条件求反比例函数和一次函数的解析式；

    (2)根据图象写出使一次函数的值大于反比例函数的值的的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

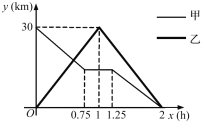
    【题目】在一条笔直的公路上有A、B两地.甲、乙两人同时出发，甲骑电动车从A地匀速前往B地，行走到一半路程时出现故障后停车维修,修好车后以原速继续行驶到B地；乙骑摩托车从B地匀速前往A地，到达A地后立即按原路原速返回，结果两人同时到B地.甲、乙两人与B地的距离y(km)与乙行驶时间x(h)之间的函数图象如图所示.

    （1）求甲修车前的速度.

    （2）求甲、乙第一次相遇的时间.

    （3）若两人之间的距离不超过10km时，能够用无线对讲机保持联系，请直接写出乙在行进中能用无线对讲机与甲保持联系的x取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为迎接“国家卫生城市”复检，某市环卫局准备购买A、B两种型号的垃圾箱，通过市场调研得知：购买3个A型垃圾箱和2个B型垃圾箱共需540元；购买2个A型垃圾箱比购买3个B型垃圾箱少用160元．

    （1）每个A型垃圾箱和B型垃圾箱各多少元？

    （2）现需要购买A，B两种型号的垃圾箱共300个，分别由甲、乙两人进行安装，要求在12天内完成（两人同时进行安装）．已知甲负责A型垃圾箱的安装，每天可以安装15个，乙负责B型垃圾箱的安装，每天可以安装20个，生产厂家表示若购买A型垃圾箱不少于150个时，该型号的产品可以打九折；若购买B型垃圾箱超过150个时，该型号的产品可以打八折，若既能在规定时间内完成任务，费用又最低，应购买A型和B型垃圾箱各多少个？最低费用是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

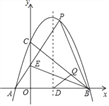
    【题目】如图，已知抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣1，0），B（4，0），与y轴交于点C（0，4）．

    （1）求此抛物线的解析式；

    （2）设点P（2，n）在此抛物线上，AP交y轴于点E，连接BE，BP，请判断△BEP的形状，并说明理由；

    （3）设抛物线的对称轴交x轴于点D，在线段BC上是否存在点Q，使得△DBQ成为等腰直角三角形？若存在，求出点Q的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

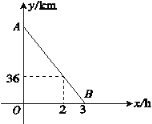
    【题目】小王骑车从甲地到乙地，小李骑车从乙地到甲地，两人同时出发，沿同一条公路匀速前进，在出发2 h时，两人相距36 km，在出发3 h时，两人相遇．设骑行的时间为x（h），两人之间的距离为y（km），图中的线段AB表示两人从出发到相遇这个过程中y与x之间的函数关系．

    （1）求线段AB所表示的y与x之间的函数表达式；

    （2）求甲、乙两地之间的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标中，点O为坐标原点，直线y=﹣x+4与x轴交于点A，过点A的抛物线y=ax2+bx与直线y=﹣x+4交于另一点B，且点B的横坐标为1．

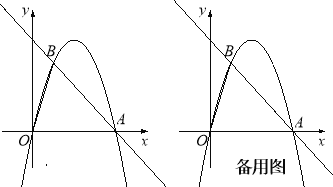
    （1）求a，b的值；

    （2）点P是线段AB上一动点（点P不与点A、B重合），过点P作PM∥OB交第一象限内的抛物线于点M，过点M作MC⊥x轴于点C，交AB于点N，过点P作PF⊥MC于点F，设PF的长为t，MN的长为d，求d与t之间的函数关系式（不要求写出自变量t的取值范围）；

    （3）在（2）的条件下，当S△ACN=S△PMN时，连接ON，点Q在线段BP上，过点Q作QR∥MN交ON于点R，连接MQ、BR，当∠MQR﹣∠BRN=45°时，求点R的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知△ABC中，∠C是其最小的内角，如果过点B的一条直线把这个三角形分割成了两个三角形，其中一个为等腰三角形，另一个为直角三角形，则称这条直线为△ABC关于点B的奇异分割线．

    例如：图1，在Rt△ABC中，∠A＝90°，∠C＝20°，过顶点B的一条直线BD交AC于点D，且∠DBC＝20°，则直线BD是△ABC的关于点B的奇异分割线．

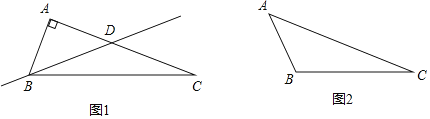
    （1）如图2，在△ABC中，若∠A＝50°，∠C＝20°．请过顶点B在图2中画出△ABC关于点B的奇异分割线BD交AC于点D，此时∠ADB＝　 　度；

    （2）在△ABC中，∠C＝30°，若△ABC存在关于点B的奇异分割线，画出相应的△ABC及分割线BD，并直接写出此时∠ABC的度数（要求在图中标注∠A、∠ABD及∠DBC的度数）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在△ABC中，AB＝AC＝4cm，将△ABC沿CA方向平移4cm得到△EFA，连接BE，BF；BE与AF交于点G

    (1)判断BE与AF的位置关系，并说明理由；

    (2)若∠BEC＝15°，求四边形BCEF的面积．

    查看答案和解析>>

    同步练习册答案