
����Ŀ����ͼ����ƽ��ֱ�������У���OΪ����ԭ�㣬ֱ��y=��x+4��x�ύ�ڵ�A������A��������y=ax2+bx��ֱ��y=��x+4������һ��B���ҵ�B�ĺ�����Ϊ1��
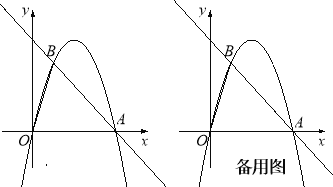
��1����a��b��ֵ��
��2����P���߶�AB��һ���㣨��P�����A��B�غϣ�������P��PM��OB����һ�����ڵ��������ڵ�M������M��MC��x���ڵ�C����AB�ڵ�N������P��PF��MC�ڵ�F����PF�ij�Ϊt��MN�ij�Ϊd����d��t֮��ĺ�����ϵʽ����Ҫ��д���Ա���t��ȡֵ��Χ����
��3���ڣ�2���������£���S��ACN=S��PMNʱ������ON����Q���߶�BP�ϣ�����Q��QR��MN��ON�ڵ�R������MQ��BR������MQR����BRN=45��ʱ�����R�����꣮
���𰸡���1��a=��1��b=4��
��2��d=3t+t=4t��
��3��R��![]() ��
��![]() ����
����
��������
�����������1������֪�ɵó�A��B�����꣬�Ӷ����ݴ���ϵ�����ó�a��b��ֵ��
��2������֪�ɵó�AD=BD���Ӷ���BAD=��ABD=45���������ɵó�tan��BOD=tan��MPF����![]() =3��MF=3PF=3t�����ɵó�d��t�ĺ�����ϵ��
=3��MF=3PF=3t�����ɵó�d��t�ĺ�����ϵ��
��3����S��ACN=S��PMN����ɵ�![]() AC2=2t2���Ӷ��ó�AC=2t��CN=2t����M��4��2t��6t�������t��ֵ�������ó���PMQ�ס�NBR�����R�����꣮
AC2=2t2���Ӷ��ó�AC=2t��CN=2t����M��4��2t��6t�������t��ֵ�������ó���PMQ�ס�NBR�����R�����꣮
�����������1����y=��x+4��x�ύ�ڵ�A��
��A��4��0����
����B�ĺ�����Ϊ1����ֱ��y=��x+4������B��
��B��1��3����
��������y=ax2+bx����A��4��0����B��1��3����
��![]() ��
��
��ã�![]() ��
��
��a=��1��b=4��
��2����ͼ����BD��x���ڵ�D���ӳ�MP��x���ڵ�E��
��B��1��3����A��4��0����
��OD=1��BD=3��OA=4��
��AD=3��
��AD=BD��
�ߡ�BDA=90������BAD=��ABD=45����
��MC��x�ᣬ���ANC=��BAD=45����
���PNF=��ANC=45����
��PF��MC�����FPN=��PNF=45����
��NF=PF=t��
�ߡ�DFM=��ECM=90������PF��EC��
���MPF=��MEC��
��ME��OB�����MEC=��BOD��
���MPF=��BOD��
��tan��BOD=tan��MPF��
��![]() =3��
=3��
��MF=3PF=3t��
��MN=MF+FN��
��d=3t+t=4t��
��3���籸��ͼ���ɣ�2��֪��PF=t��MN=4t��
��S��PMN=![]() MN��PF=
MN��PF=![]() ��4t��t=2t2��
��4t��t=2t2��
�ߡ�CAN=��ANC��
��CN=AC��
��S��ACN=![]() AC2��
AC2��
��S��ACN=S��PMN��
��![]() AC2=2t2��
AC2=2t2��
��AC=2t����CN=2t��
��MC=MN+CN=6t��
��OC=OA��AC=4��2t��
��M��4��2t��6t����
�ɣ�1��֪�����ߵĽ���ʽΪ��y=��x2+4x��
��M��4��2t��6t������y=��x2+4x�ã�
����4��2t��2+4��4��2t��=6t��
��ã�t1=0���ᣩ��t2=![]() ��
��
��PF=NF=![]() ��AC=CN=1��OC=3��MF=
��AC=CN=1��OC=3��MF=![]() ��PN=
��PN=![]() ��PM=
��PM=![]() ��AN=
��AN=![]() ��
��
��AB=3![]() ��
��
��BN=2![]() ��
��
��NH��RQ�ڵ�H��
��QR��MN��
���MNH=��RHN=90����
��RQN=��QNM=45�������MNH=��NCO��
��NH��OC��
���HNR=��NOC��
��tan��HNR=tan��NOC��
��![]() ��
��
��RH=n����HN=3n��
��RN=![]() n��QN=3
n��QN=3![]() n��
n��
��PQ=QN��PN=3![]() n��
n��![]() ��
��
��ON=![]() ��
��
OB=![]() ��
��
��OB=ON�����OBN=��BNO��
��PM��OB��
���OBN=��MPB��
���MPB=��BNO��
�ߡ�MQR����BRN=45������MQR=��MQP+��RQN=��MQP+45����
���BRN=��MQP��
���PMQ�ס�NBR��
��![]() ��
��
�� ��
��
��ã�n=![]() ��
��
��R�ĺ�����Ϊ��3��![]() ��R��������Ϊ��1��
��R����������1��![]() =
=![]() ��
��
��R��![]() ��
��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
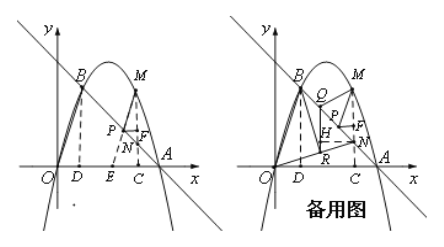
����Ŀ����ͼ��AB�ǡ�O��ֱ������P����AC��һ���㣨����A��C�غϣ�������P��PE��AB������ΪE������EP����AC�ڵ�F��������C�������ڵ�D��
��1����֤��DC��DP��
��2������CAB��30������F�ǻ�AC���е�ʱ���ж���A��O��C��FΪ������ı�����ʲô�����ı��Σ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=��x+4��ͼ���뷴��������y=![]() ��kΪ��������k��0����ͼ����A��1��a����B���㣮
��kΪ��������k��0����ͼ����A��1��a����B���㣮
��1�����������ı���ʽ����B�����ꣻ
��2����x������һ��P��ʹPA+PB��ֵ��С�������������ĵ�P�����꼰��PAB�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ����ݲ��ϻش�
����1��![]()
![]()
![]()
![]()
![]() .
.
����2��
8![]() ��0.125
��0.125![]() ��8��8��8��8��8��8��0.125��0.125��0.125��0.125��0.125��0.125
��8��8��8��8��8��8��0.125��0.125��0.125��0.125��0.125��0.125
��(8��0.125)��(8��0.125)��(8��0.125)��(8��0.125)��(8��0.125)��(8��0.125)
��(8��0.125)6 ��1.
��1������������ϵļ��㷽�����㣺![]() ��
��
��2��������ļ�����ܽ��һ�����ɣ�(����ĸ��ʾ) ![]() ��
��
��3���ã�2���Ĺ��ɼ��㣺![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
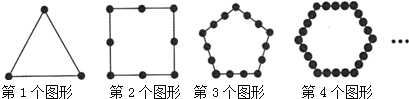
����Ŀ����ͼ��ʾ����ͬ����С�ĺ�ɫ���Ӱڷ���������εı��ϣ����������Ĺ��ɰ���ȥ����� n��ͼ����Ҫ��ɫ���ӵĸ�����______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD��ƽ���ı�������AB'C����ABC����AC���ڵ�ֱ�߶Գ���AD��B'C�ཻ�ڵ�O������BB'
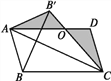
��1����ֱ��д��ͼ�����еĵ�������������������ĸ����
��2����֤����AB'O����CDO
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����ͬѧ��A�س����������г���ͬһ��·����ʻ��B�أ�����������صľ���s��ǧ�ף�����ʻʱ��t��Сʱ��֮��ĺ�����ϵͼ����ͼ��ʾ������ͼ���ṩ����Ϣ��������˵����

��1�����Ƕ���ʻ��18ǧ�ף�
��2������;��ͣ����0.5Сʱ��
��3���ұȼ���������0.5Сʱ��
��4���������ٶ�С���ҵ��ٶȣ�
��5���ס�������ͬʱ����Ŀ�ĵ�
���з���ͼ��������˵���У� ��
A. 2��B. 3��C. 4��D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
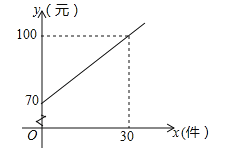
����Ŀ��ij��ݹ�˾��ÿλ�����С�硱��������ÿ�յ���������һ�κ�����ϵ����ͼ��ʾ��
��1����ÿλ�����С�硱��������y��Ԫ������������x������֮��ĺ�����ϵʽ��
��2����֪ij�����С�硱�������벻����110Ԫ����������Ҫ���Ͷ��ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
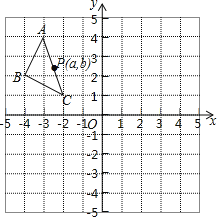
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC���������������ֱ�ΪA��-3,4��,B��-4,2����C��-2,1�����ҡ�A1B1C1���ABC����ԭ��O�����ĶԳơ�
��1��������A1B1C1����д����A1�����ꣻ
��2��P��a,b���ǡ�ABC��AC����һ�㣬��ABC��ƽ�ƺ��P�Ķ�Ӧ��ΪP����a+3,b+1�����뻭��ƽ�ƺ�ġ�A2B2C2.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com