
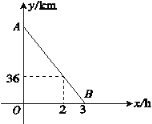
����Ŀ��С���ﳵ�Ӽص��ҵأ�С���ﳵ���ҵص��أ�����ͬʱ��������ͬһ����·����ǰ�����ڳ���2 hʱ���������36 km���ڳ���3 hʱ�����������������е�ʱ��Ϊx��h��������֮��ľ���Ϊy��km����ͼ�е��߶�AB��ʾ���˴ӳ������������������y��x֮��ĺ�����ϵ��
��1�����߶�AB����ʾ��y��x֮��ĺ�������ʽ��
��2����ס�������֮��ľ��룮
 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д� �㾦�½̲�ȫ�ܽ��ϵ�д�
�㾦�½̲�ȫ�ܽ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD�ǡ�ABC�����ߣ�E��F�ֱ���AD��AD�ӳ����ϵĵ㣬��DE=DF������BF��CE.����˵�����١�ABD�͡�ACD�����ȣ��ڡ�BAD=��CAD���ۡ�BDF�ա�CDE����BF��CE��������ȷ���У�������
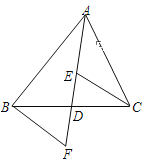
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ������C��D�ǰ�ԲO�����ȷֵ㣬����C����O�����߽�AD���ӳ����ڵ�E������D��DF��AB�ڵ�F������O�ڵ�H������DC��AC��
��1����֤����AEC=90�㣻
��2�����ж��Ե�A��O��C��DΪ������ı��ε���״����˵�����ɣ�
��3����DC=2����DH�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b��ͼ����A����2��6��������x���ཻ�ڵ�B��������������y=3x��ͼ���ཻ�ڵ�C����C�ĺ�����Ϊ1��
��1����k��b��ֵ��
��2������D��y�Ḻ�����ϣ�������S��COD=![]() S��BOC�����D�����꣮
S��BOC�����D�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ����ݲ��ϻش�
����1��![]()
![]()
![]()
![]()
![]() .
.
����2��
8![]() ��0.125
��0.125![]() ��8��8��8��8��8��8��0.125��0.125��0.125��0.125��0.125��0.125
��8��8��8��8��8��8��0.125��0.125��0.125��0.125��0.125��0.125
��(8��0.125)��(8��0.125)��(8��0.125)��(8��0.125)��(8��0.125)��(8��0.125)
��(8��0.125)6 ��1.
��1������������ϵļ��㷽�����㣺![]() ��
��
��2��������ļ�����ܽ��һ�����ɣ�(����ĸ��ʾ) ![]() ��
��
��3���ã�2���Ĺ��ɼ��㣺![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��618���д�ٻ�У�������̷��ڽ��н��۴�����ij��������������A���װ���м۸�����������۱�ƽʱ�ۼ�ÿ����90Ԫ�����������ͬ������A���װ��ƽʱ���۶�Ϊ5��Ԫ�����������۶�ֻ��4��Ԫ��
(1)�õ���A���װƽʱÿ���ۼ�Ϊ����Ԫ?
(2)�õ�����6��1��6��2��һ�ִ����У�A���װ����������dz��𱬣��̼Ҿ���Ϊ�ڶ���6��16��6��18����ٽ�һ����������A���ͬʱ�ٹ���ͬƷ�Ƶ�B���װ����֪A���װÿ������Ϊ300Ԫ��B���װÿ������Ϊ200Ԫ������Ԥ���ò�����7.2��Ԫ�Ҳ�����7.3��Ԫ���ʽ��������װ��300����������һ�㣬�̼ҹ��м��ֽ�������?
(3)��6��16��6��18������У�A������ƽ�ռ۽�90Ԫ������B���װÿ���ۼ�Ϊ280Ԫ��Ϊ��B���װ����·�����̾���ÿ�۳�һ��B���װ�������˿��ֽ�![]() Ԫ��Ҫʹ(2)����������װȫ����������з���������ͬ��
Ԫ��Ҫʹ(2)����������װȫ����������з���������ͬ��![]() ��ֵӦ�Ƕ���?
��ֵӦ�Ƕ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD��ƽ���ı�������AB'C����ABC����AC���ڵ�ֱ�߶Գ���AD��B'C�ཻ�ڵ�O������BB'
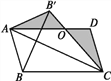
��1����ֱ��д��ͼ�����еĵ�������������������ĸ����
��2����֤����AB'O����CDO
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺����ABC�У�����һ���ڽ�����һ���ڽǵ�һ�룬�����ABCΪ������������������ݴ˶��壬���������⣺
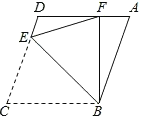
��1������ABCΪ��������Σ��ҡ�A��90��������ABC�����������ǵĶ���Ϊ�� ����
��2������ABC�ǰ�������Σ��ҡ�C��40�������B�� ����
��3����ͼ�����ı���ABCD�У�AB��CD��AD��BC����C��72������E�ڱ�CD�ϣ���BEΪ�ۺۣ�����BCE���Ϸ��ۣ���Cǡ������AD���ϵĵ�F����BF��AD������EDF�ǰ�������������ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2018�����������λ�У�ij�����ƻ������Ϊ1600m2����������̻�����Ͷ�꣬�ɼס����������̶�����ɣ�����ÿ��������̻���������Ҷ�ÿ��������̻������2���������ڶ���������Ϊ400m2������̻�ʱ���ӱ��Ҷ�����5�죮
(1)��ס��������̶�ÿ��������̻��������
(2)����̶�ʩ��x�죬�ҹ��̶�ʩ��y�죬�պ�����̻�������y����x�ĺ�����ϵʽ��
(3)����ÿ���̻�������0.6��Ԫ���Ҷ�ÿ���̻�����Ϊ0.25��Ԫ���Ҽ�������ʩ����������������25�죬����ΰ��ż�������ʩ����������ʹʩ���ܷ�����ͣ��������ͷ��ã�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com