
【题目】如图,AB是⊙O的直径,点C,D是半圆O的三等分点,过点C作⊙O的切线交AD的延长线于点E,过点D作DF⊥AB于点F,交⊙O于点H,连接DC,AC.
(1)求证:∠AEC=90°;
(2)试判断以点A,O,C,D为顶点的四边形的形状,并说明理由;
(3)若DC=2,求DH的长.

【答案】(1)证明见解析;
(2)四边形AOCD为菱形;
(3)DH=2![]() .
.
【解析】
试题分析:(1)连接OC,根据EC与⊙O切点C,则∠OCE=90°,由题意得![]() ,∠DAC=∠CAB,即可证明AE∥OC,则∠AEC+∠OCE=180°,从而得出∠AEC=90°;
,∠DAC=∠CAB,即可证明AE∥OC,则∠AEC+∠OCE=180°,从而得出∠AEC=90°;
(2)四边形AOCD为菱形.由(1)得![]() ,则∠DCA=∠CAB可证明四边形AOCD是平行四边形,再由OA=OC,即可证明平行四边形AOCD是菱形(一组邻边相等的平行四边形是菱形);
,则∠DCA=∠CAB可证明四边形AOCD是平行四边形,再由OA=OC,即可证明平行四边形AOCD是菱形(一组邻边相等的平行四边形是菱形);
(3)连接OD.根据四边形AOCD为菱形,得△OAD是等边三角形,则∠AOD=60°,再由DH⊥AB于点F,AB为直径,在Rt△OFD中,根据sin∠AOD=![]() ,求得DH的长.
,求得DH的长.
试题解析:(1)连接OC,
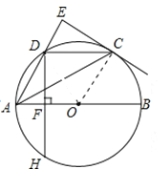
∵EC与⊙O切点C,
∴OC⊥EC,
∴∠OCE=90°,
∵点CD是半圆O的三等分点,
∴![]() ,
,
∴∠DAC=∠CAB,
∵OA=OC,
∴∠CAB=∠OCA,
∴∠DAC=∠OCA,
∴AE∥OC(内错角相等,两直线平行)
∴∠AEC+∠OCE=180°,
∴∠AEC=90°;
(2)四边形AOCD为菱形.理由是:
∵![]() ,
,
∴∠DCA=∠CAB,
∴CD∥OA,
又∵AE∥OC,
∴四边形AOCD是平行四边形,
∵OA=OC,
∴平行四边形AOCD是菱形(一组邻边相等的平行四边形是菱形);
(3)连接OD.
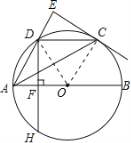
∵四边形AOCD为菱形,
∴OA=AD=DC=2,
∵OA=OD,
∴OA=OD=AD=2,
∴△OAD是等边三角形,
∴∠AOD=60°,
∵DH⊥AB于点F,AB为直径,
∴DH=2DF,
在Rt△OFD中,sin∠AOD=![]() ,
,
∴DF=ODsin∠AOD=2sin60°=![]() ,
,
∴DH=2DF=2![]() .
.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点,且点
两点,且点![]() 的坐标为
的坐标为![]() ,将直线
,将直线![]() 向上平移
向上平移![]() 个单位,交双曲线
个单位,交双曲线![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且
,且![]() 的面积是
的面积是![]() .给出以下结论:(1)
.给出以下结论:(1)![]() ;(2)点
;(2)点![]() 的坐标是
的坐标是![]() ;(3)
;(3)![]() ;(4)
;(4)![]() .其中正确的结论有
.其中正确的结论有![]()
![]()
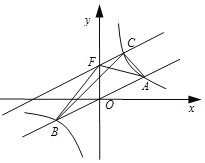
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
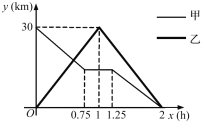
【题目】在一条笔直的公路上有A、B两地.甲、乙两人同时出发,甲骑电动车从A地匀速前往B地,行走到一半路程时出现故障后停车维修,修好车后以原速继续行驶到B地;乙骑摩托车从B地匀速前往A地,到达A地后立即按原路原速返回,结果两人同时到B地.甲、乙两人与B地的距离y(km)与乙行驶时间x(h)之间的函数图象如图所示.
(1)求甲修车前的速度.
(2)求甲、乙第一次相遇的时间.
(3)若两人之间的距离不超过10km时,能够用无线对讲机保持联系,请直接写出乙在行进中能用无线对讲机与甲保持联系的x取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(﹣1,0).有下列结论:
①abc>0;②4a﹣2b+c<0;③4a+b=0;④抛物线与x轴的另一个交点是(5,0);⑤点(﹣3,y1),(6,y2)都在抛物线上,则有y1<y2.
其中正确的是( )
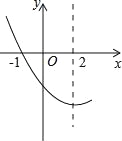
A.①②③ B.②④⑤ C.①③④ D.③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接“国家卫生城市”复检,某市环卫局准备购买A、B两种型号的垃圾箱,通过市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需540元;购买2个A型垃圾箱比购买3个B型垃圾箱少用160元.
(1)每个A型垃圾箱和B型垃圾箱各多少元?
(2)现需要购买A,B两种型号的垃圾箱共300个,分别由甲、乙两人进行安装,要求在12天内完成(两人同时进行安装).已知甲负责A型垃圾箱的安装,每天可以安装15个,乙负责B型垃圾箱的安装,每天可以安装20个,生产厂家表示若购买A型垃圾箱不少于150个时,该型号的产品可以打九折;若购买B型垃圾箱超过150个时,该型号的产品可以打八折,若既能在规定时间内完成任务,费用又最低,应购买A型和B型垃圾箱各多少个?最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
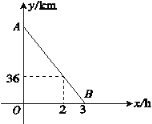
【题目】小王骑车从甲地到乙地,小李骑车从乙地到甲地,两人同时出发,沿同一条公路匀速前进,在出发2 h时,两人相距36 km,在出发3 h时,两人相遇.设骑行的时间为x(h),两人之间的距离为y(km),图中的线段AB表示两人从出发到相遇这个过程中y与x之间的函数关系.
(1)求线段AB所表示的y与x之间的函数表达式;
(2)求甲、乙两地之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
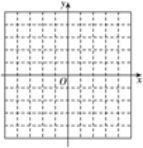
【题目】已知正比例函数![]() 的图象经过点(3,-6).
的图象经过点(3,-6).
(1)求这个函数的表达式;
(2)在如图所示的直角坐标系中画出这个函数的图象;
(3)判断点A(4,-2)、B(-1.5,3)是否在这个函数的图象上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com