
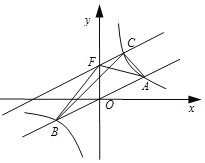
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点,且点
两点,且点![]() 的坐标为
的坐标为![]() ,将直线
,将直线![]() 向上平移
向上平移![]() 个单位,交双曲线
个单位,交双曲线![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且
,且![]() 的面积是
的面积是![]() .给出以下结论:(1)
.给出以下结论:(1)![]() ;(2)点
;(2)点![]() 的坐标是
的坐标是![]() ;(3)
;(3)![]() ;(4)
;(4)![]() .其中正确的结论有
.其中正确的结论有![]()
![]()
A. 1个B. 2个C. 3个D. 4个
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,∠BAD=90°,CE⊥AD于点E,AD=8cm,BC=4cm,AB=5cm.从初始时刻开始,动点P,Q 分别从点A,B同时出发,运动速度均为1cm/s,动点P沿A﹣B﹣﹣C﹣﹣E的方向运动,到点E停止;动点Q沿B﹣﹣C﹣﹣E﹣﹣D的方向运动,到点D停止,设运动时间为xs,△PAQ的面积为ycm2,(这里规定:线段是面积为0的三角形)
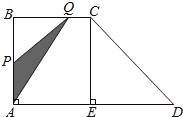
解答下列问题:
(1)当x=2s时,y= cm2;当x=![]() s时,y= cm2.
s时,y= cm2.
(2)当5≤x≤14 时,求y与x之间的函数关系式.
(3)当动点P在线段BC上运动时,求出![]() 时x的值.
时x的值.
(4)直接写出在整个运动过程中,使PQ与四边形ABCE的对角线平行的所有x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学问题:用边长相等的正三角形、正方形和正六边形能否进行平面图形的镶嵌?
问题探究:为了解决上述数学问题,我们采用分类讨论的思想方法去进行探究.
探究一:从正三角形、正方形和正六边形中任选一种图形,能否进行平面图形的镶嵌?
第一类:选正三角形.因为正三角形的每一个内角是60°,所以在镶嵌平面时,围绕某一点有6个正三角形的内角可以拼成一个周角,所以用正三角形可以进行平面图形的镶嵌.
第二类:选正方形.因为正方形的每一个内角是90°,所以在镶嵌平面时,围绕某一点有4个正方形的内角可以拼成一个周角,所以用正方形也可以进行平面图形的镶嵌.
第三类:选正六边形.(仿照上述方法,写出探究过程及结论)
探究二:从正三角形、正方形和正六边形中任选两种图形,能否进行平面图形的镶嵌?
第四类:选正三角形和正方形
在镶嵌平面时,设围绕某一点有x个正三角形和y个正方形的内角可以拼成个周角.根据题意,可得方程
60x+90y=360
整理,得2x+3y=12.
我们可以找到唯一组适合方程的正整数解为![]() .
.
镶嵌平面时,在一个顶点周围围绕着3个正三角形和2个正方形的内角可以拼成一个周角,所以用正三角形和正方形可以进行平面镶嵌
第五类:选正三角形和正六边形.(仿照上述方法,写出探究过程及结论)
第六类:选正方形和正六边形,(不写探究过程,只写出结论)
探究三:用正三角形、正方形和正六边形三种图形是否可以镶嵌平面?
第七类:选正三角形、正方形和正六边形三种图形.(不写探究过程,只写结论),
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在研究数学问题时遇到一个定义:将三个已经排好顺序的数:![]() ,
,![]() ,
,![]() ,称为数列
,称为数列![]() ,
,![]() ,
,![]() .计算
.计算![]() ,
,![]() ,
,![]() ,将这三个数的最小值称为数列
,将这三个数的最小值称为数列![]() ,
,![]() ,
,![]() 的最佳值.例如,对于数列2,
的最佳值.例如,对于数列2,![]() ,3,因为
,3,因为![]() ,
,![]() ,
,![]() ,所以数列2,
,所以数列2,![]() ,3的最佳值为
,3的最佳值为![]() .
.
小明进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的最佳值.如数列![]() ,2,3的最佳值为
,2,3的最佳值为![]() ;数列3,
;数列3,![]() ,2的最佳值为1;
,2的最佳值为1;![]() .经过研究,小明发现,对于“2,
.经过研究,小明发现,对于“2,![]() ,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为
,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)求数列![]() ,
,![]() ,2的最佳值;
,2的最佳值;
(2)将“![]() ,
,![]() ,1”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为 ,取得最佳值最小值的数列为 (写出一个即可);
,1”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为 ,取得最佳值最小值的数列为 (写出一个即可);
(3)将3,![]() ,
,![]() 这三个数按照不同的顺序排列,可得到若干个数列.若使数列的最佳值为1,求
这三个数按照不同的顺序排列,可得到若干个数列.若使数列的最佳值为1,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材母题 点P(x,y)在第一象限,且x+y=8,点A的坐标为(6,0).设△OPA的面积为S.
(1)用含有x的式子表示S,写出x的取值范围,画出函数S的图象;
(2)当点P的横坐标为5时,△OPA的面积为多少?
(3)△OPA的面积能大于24吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
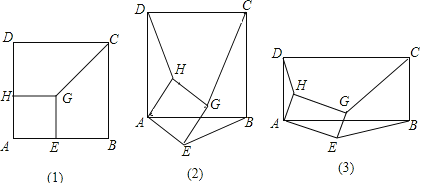
【题目】![]() 如图
如图![]() ,正方形AEGH的顶点E、H在正方形ABCD的边上,直接写出HD:GC:EB的结果______;
,正方形AEGH的顶点E、H在正方形ABCD的边上,直接写出HD:GC:EB的结果______;
![]() 将图
将图![]() 中的正方形AEGH绕点A旋转一定角度,如图
中的正方形AEGH绕点A旋转一定角度,如图![]() ,求HD:GC:EB;
,求HD:GC:EB;
![]() 把图
把图![]() 中的正方形都换成矩形,如图
中的正方形都换成矩形,如图![]() ,且已知DA:
,且已知DA:![]() :
:![]() ,求此时HD:GC:EB的值
,求此时HD:GC:EB的值![]() 简要写出过程
简要写出过程![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法:①△ABD和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;其中正确的有( )
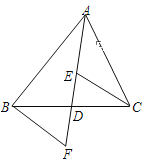
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C,D是半圆O的三等分点,过点C作⊙O的切线交AD的延长线于点E,过点D作DF⊥AB于点F,交⊙O于点H,连接DC,AC.
(1)求证:∠AEC=90°;
(2)试判断以点A,O,C,D为顶点的四边形的形状,并说明理由;
(3)若DC=2,求DH的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com