
����Ŀ��Ϊӭ���������������������죬ij�л�����������A��B�����ͺŵ������䣬ͨ���г����е�֪������3��A���������2��B�������乲��540Ԫ������2��A��������ȹ���3��B������������160Ԫ��
��1��ÿ��A���������B�������������Ԫ��
��2������Ҫ����A��B�����ͺŵ������乲300�����ֱ��ɼס������˽��а�װ��Ҫ����12������ɣ�����ͬʱ���а�װ������֪����A��������İ�װ��ÿ�����װ15�����Ҹ���B��������İ�װ��ÿ�����װ20�����������ұ�ʾ������A�������䲻����150��ʱ�����ͺŵIJ�Ʒ���Դ���ۣ�������B�������䳬��150��ʱ�����ͺŵIJ�Ʒ���Դ���ۣ��������ڹ涨ʱ�����������������ͣ�Ӧ����A�ͺ�B������������ٸ�����ͷ����Ƕ���Ԫ��
���𰸡�(1) A���������B��������ֱ�Ϊ100Ԫ��120Ԫ����2��A��������60����B��������240��ʱ����ͷ���Ϊ29040Ԫ��
����������������1����ÿ��A���������B��������ֱ�ΪxԪ��yԪ���������ι���ķ����з���![]() ��Ȼ��ⷽ���鼴�ɣ�
��Ȼ��ⷽ���鼴�ɣ�
��2���蹺��A��������m��������B�������䣨300-m����������������ķ���ΪwԪ�����ù���Ч�ʺ��ܹ���ʱ��ɵõ�60��m��180��Ȼ�����ۣ���60��m<150�õ�w=4m+28800����150��m��180��w=-30m+3600��������һ�κ��������������������µ�w����Сֵ�����DZȽϴ�С�ɵõ����������Ĺ�����
��⣺��1����ÿ��A���������B��������ֱ�ΪxԪ��yԪ��
���������![]() ,���
,���![]() ��
��
��ÿ��A���������B��������ֱ�Ϊ100Ԫ��120Ԫ��
��2���蹺��A��������m��������B���������������������ķ���ΪwԪ��
���������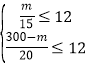 �����60��m��180��
�����60��m��180��
��60��m��150��w=100m+120��0.8��=4m+28800��
��m=60ʱ��w��С��w����Сֵ=4��60+28800=29040��Ԫ����
��150��m��180��w=100��0.9��m+120��=��30m+36000��
��m=180��w��С��w����Сֵ=��30��180+36000=30600��Ԫ����
��29040��30600��
���A��������60��������B��������240��ʱ�������ڹ涨ʱ�����������������ͣ���ͷ���Ϊ29040Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() ��ͼ
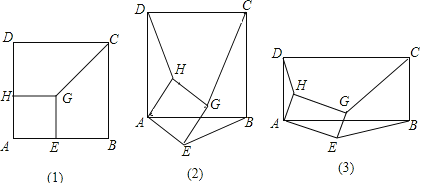
��ͼ![]() ��������AEGH�Ķ���E��H��������ABCD�ı��ϣ�ֱ��д��HD��GC��EB�Ľ��______��
��������AEGH�Ķ���E��H��������ABCD�ı��ϣ�ֱ��д��HD��GC��EB�Ľ��______��
![]() ��ͼ
��ͼ![]() �е�������AEGH�Ƶ�A��תһ���Ƕȣ���ͼ
�е�������AEGH�Ƶ�A��תһ���Ƕȣ���ͼ![]() ����HD��GC��EB��
����HD��GC��EB��
![]() ��ͼ
��ͼ![]() �е������ζ����ɾ��Σ���ͼ
�е������ζ����ɾ��Σ���ͼ![]() ������֪DA��
������֪DA��![]() ��
��![]() �����ʱHD��GC��EB��ֵ
�����ʱHD��GC��EB��ֵ![]() ��Ҫд������
��Ҫд������![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
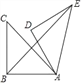
����Ŀ����ͼ����Rt��ABC�У���ABC=90����AB=BC=4������ABC���Ƶ�A˳ʱ����ת60�����õ���ADE������BE����BE�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ������C��D�ǰ�ԲO�����ȷֵ㣬����C����O�����߽�AD���ӳ����ڵ�E������D��DF��AB�ڵ�F������O�ڵ�H������DC��AC��
��1����֤����AEC=90�㣻
��2�����ж��Ե�A��O��C��DΪ������ı��ε���״����˵�����ɣ�
��3����DC=2����DH�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=��x+4��ͼ���뷴��������y=![]() ��kΪ��������k��0����ͼ����A��1��a����B���㣮
��kΪ��������k��0����ͼ����A��1��a����B���㣮
��1�����������ı���ʽ����B�����ꣻ
��2����x������һ��P��ʹPA+PB��ֵ��С�������������ĵ�P�����꼰��PAB�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b��ͼ����A����2��6��������x���ཻ�ڵ�B��������������y=3x��ͼ���ཻ�ڵ�C����C�ĺ�����Ϊ1��
��1����k��b��ֵ��
��2������D��y�Ḻ�����ϣ�������S��COD=![]() S��BOC�����D�����꣮
S��BOC�����D�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ����ݲ��ϻش�
����1��![]()
![]()
![]()
![]()
![]() .
.
����2��
8![]() ��0.125
��0.125![]() ��8��8��8��8��8��8��0.125��0.125��0.125��0.125��0.125��0.125
��8��8��8��8��8��8��0.125��0.125��0.125��0.125��0.125��0.125
��(8��0.125)��(8��0.125)��(8��0.125)��(8��0.125)��(8��0.125)��(8��0.125)
��(8��0.125)6 ��1.
��1������������ϵļ��㷽�����㣺![]() ��
��
��2��������ļ�����ܽ��һ�����ɣ�(����ĸ��ʾ) ![]() ��
��
��3���ã�2���Ĺ��ɼ��㣺![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD��ƽ���ı�������AB'C����ABC����AC���ڵ�ֱ�߶Գ���AD��B'C�ཻ�ڵ�O������BB'
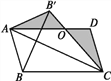
��1����ֱ��д��ͼ�����еĵ�������������������ĸ����
��2����֤����AB'O����CDO
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ����̽���������еĹ��ɲ�����������⣺
����̽���������еĹ��ɲ�����������⣺
��1��![]() ��
��![]() ������
������![]() ____________
____________
��2���۲������������
1
3 5
7 9 11 13
15 17 19 21 23 25 27 29
�� ��
��2019�Ǹ������еĵ�![]() ���еĵ�
���еĵ�![]() ��������
��������![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com