
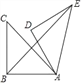
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC=4,将△ABC△绕点A顺时针旋转60°,得到△ADE,连结BE,则BE的长为_____.
【答案】![]() .
.
【解析】解:连结CE,设BE与AC相交于点F,如下图所示,

∵Rt△ABC中,AB=BC,∠ABC=90°,
∴∠BCA=∠BAC=45°,
∵Rt△ABC绕点A逆时针旋转60°与Rt△ADE重合,
∴∠BAC=∠DAE=45°,AC=AE,
又∵旋转角为60°,
∴∠BAD=∠CAE=60°,
∴△ACE是等边三角形
∴AC=CE=AE=4![]() ,
,
在△ABE与△CBE中, 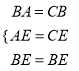 ,
,
∴△ABE≌△CBE,
∴∠ABE=∠CBE=45°,∠CEB=∠AEB=30°,
∴在△ABF中,∠BFA=180°﹣45°﹣45°=90°,
∴∠AFB=∠AFE=90°,
在Rt△ABF中,由勾股定理得,
BF=AF=![]() AB=2
AB=2![]() ,
,
又在Rt△AFE中,∠AEF=30°,∠AFE=90°,
∴FE=![]() AF=2
AF=2![]() ,
,
∴BE=BF+FE=![]() .
.
故答案为: ![]() .
.


科目:初中数学 来源: 题型:
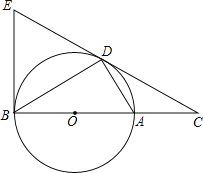
【题目】如图,D为![]() 上一点,点C在直径BA的延长线上,且
上一点,点C在直径BA的延长线上,且![]() .
.
![]() 判断直线CD与
判断直线CD与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
![]() 过点B作的
过点B作的![]() 切线交CD的延长线于点E,若
切线交CD的延长线于点E,若![]() ,
,![]() ,求
,求![]() 的半径长.
的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
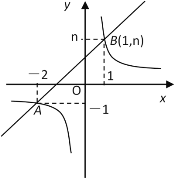
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于A(-2,-1)、B(1,n)两点。
的图象交于A(-2,-1)、B(1,n)两点。
(1)利用图中条件求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值大于反比例函数的值的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB上顺次有三个点C,D,E,把线段AB分为了2:3:4:5四部分,且AB=28,
![]()
(1)求线段AE的长;
(2)若M,N分别是DE,EB的中点,求线段MN的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有A、B两地.甲、乙两人同时出发,甲骑电动车从A地匀速前往B地,行走到一半路程时出现故障后停车维修,修好车后以原速继续行驶到B地;乙骑摩托车从B地匀速前往A地,到达A地后立即按原路原速返回,结果两人同时到B地.甲、乙两人与B地的距离y(km)与乙行驶时间x(h)之间的函数图象如图所示.
(1)求甲修车前的速度.
(2)求甲、乙第一次相遇的时间.
(3)若两人之间的距离不超过10km时,能够用无线对讲机保持联系,请直接写出乙在行进中能用无线对讲机与甲保持联系的x取值范围.
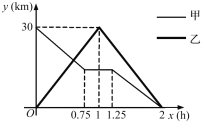
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接“国家卫生城市”复检,某市环卫局准备购买A、B两种型号的垃圾箱,通过市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需540元;购买2个A型垃圾箱比购买3个B型垃圾箱少用160元.
(1)每个A型垃圾箱和B型垃圾箱各多少元?
(2)现需要购买A,B两种型号的垃圾箱共300个,分别由甲、乙两人进行安装,要求在12天内完成(两人同时进行安装).已知甲负责A型垃圾箱的安装,每天可以安装15个,乙负责B型垃圾箱的安装,每天可以安装20个,生产厂家表示若购买A型垃圾箱不少于150个时,该型号的产品可以打九折;若购买B型垃圾箱超过150个时,该型号的产品可以打八折,若既能在规定时间内完成任务,费用又最低,应购买A型和B型垃圾箱各多少个?最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠C是其最小的内角,如果过点B的一条直线把这个三角形分割成了两个三角形,其中一个为等腰三角形,另一个为直角三角形,则称这条直线为△ABC关于点B的奇异分割线.
例如:图1,在Rt△ABC中,∠A=90°,∠C=20°,过顶点B的一条直线BD交AC于点D,且∠DBC=20°,则直线BD是△ABC的关于点B的奇异分割线.
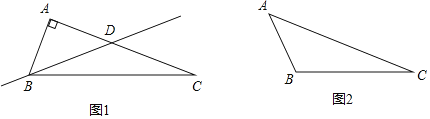
(1)如图2,在△ABC中,若∠A=50°,∠C=20°.请过顶点B在图2中画出△ABC关于点B的奇异分割线BD交AC于点D,此时∠ADB= 度;
(2)在△ABC中,∠C=30°,若△ABC存在关于点B的奇异分割线,画出相应的△ABC及分割线BD,并直接写出此时∠ABC的度数(要求在图中标注∠A、∠ABD及∠DBC的度数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com