
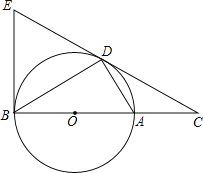
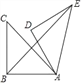
【题目】如图,D为![]() 上一点,点C在直径BA的延长线上,且
上一点,点C在直径BA的延长线上,且![]() .
.
![]() 判断直线CD与
判断直线CD与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
![]() 过点B作的
过点B作的![]() 切线交CD的延长线于点E,若
切线交CD的延长线于点E,若![]() ,
,![]() ,求
,求![]() 的半径长.
的半径长.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,∠AOB是一钢架,∠AOB=15°,为使钢架更加牢固,需在其内部添加一些钢管EF、FG、GH…添的钢管长度都与OE相等,则最多能添加这样的钢管( )根.

A. 2 B. 4 C. 5 D. 无数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过30立方米时,按2元/立方米计费;月用水量超过30立方米时,其中的30立方米仍按2元/立方米收费,超过部分按2.5元/立方米计费.设每户家庭月用水量为x立方米.
(1)当x不超过30时,应收多少水费(用x的代数式表示);当x超过30时,应收多少水费(用x的代数式表示);
(2)小明家四月份用水20立方米,五月份用水36立方米,请帮小明计算一下他家这两个月一共应交多少元水费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,∠BAD=90°,CE⊥AD于点E,AD=8cm,BC=4cm,AB=5cm.从初始时刻开始,动点P,Q 分别从点A,B同时出发,运动速度均为1cm/s,动点P沿A﹣B﹣﹣C﹣﹣E的方向运动,到点E停止;动点Q沿B﹣﹣C﹣﹣E﹣﹣D的方向运动,到点D停止,设运动时间为xs,△PAQ的面积为ycm2,(这里规定:线段是面积为0的三角形)
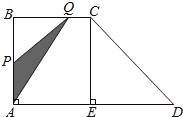
解答下列问题:
(1)当x=2s时,y= cm2;当x=![]() s时,y= cm2.
s时,y= cm2.
(2)当5≤x≤14 时,求y与x之间的函数关系式.
(3)当动点P在线段BC上运动时,求出![]() 时x的值.
时x的值.
(4)直接写出在整个运动过程中,使PQ与四边形ABCE的对角线平行的所有x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
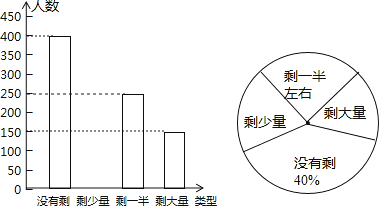
(1)这次被调查的同学共有 名;“剩大量”的扇形圆心角是 .
(2)把条形统计图补充完整;
(3)在被调查的学生中随机抽取一名恰巧是“剩少量”或“剩一半左右”饭的概率多大;
(4)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学问题:用边长相等的正三角形、正方形和正六边形能否进行平面图形的镶嵌?
问题探究:为了解决上述数学问题,我们采用分类讨论的思想方法去进行探究.
探究一:从正三角形、正方形和正六边形中任选一种图形,能否进行平面图形的镶嵌?
第一类:选正三角形.因为正三角形的每一个内角是60°,所以在镶嵌平面时,围绕某一点有6个正三角形的内角可以拼成一个周角,所以用正三角形可以进行平面图形的镶嵌.
第二类:选正方形.因为正方形的每一个内角是90°,所以在镶嵌平面时,围绕某一点有4个正方形的内角可以拼成一个周角,所以用正方形也可以进行平面图形的镶嵌.
第三类:选正六边形.(仿照上述方法,写出探究过程及结论)
探究二:从正三角形、正方形和正六边形中任选两种图形,能否进行平面图形的镶嵌?
第四类:选正三角形和正方形
在镶嵌平面时,设围绕某一点有x个正三角形和y个正方形的内角可以拼成个周角.根据题意,可得方程
60x+90y=360
整理,得2x+3y=12.
我们可以找到唯一组适合方程的正整数解为![]() .
.
镶嵌平面时,在一个顶点周围围绕着3个正三角形和2个正方形的内角可以拼成一个周角,所以用正三角形和正方形可以进行平面镶嵌
第五类:选正三角形和正六边形.(仿照上述方法,写出探究过程及结论)
第六类:选正方形和正六边形,(不写探究过程,只写出结论)
探究三:用正三角形、正方形和正六边形三种图形是否可以镶嵌平面?
第七类:选正三角形、正方形和正六边形三种图形.(不写探究过程,只写结论),
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在研究数学问题时遇到一个定义:将三个已经排好顺序的数:![]() ,
,![]() ,
,![]() ,称为数列
,称为数列![]() ,
,![]() ,
,![]() .计算
.计算![]() ,
,![]() ,
,![]() ,将这三个数的最小值称为数列
,将这三个数的最小值称为数列![]() ,
,![]() ,
,![]() 的最佳值.例如,对于数列2,
的最佳值.例如,对于数列2,![]() ,3,因为
,3,因为![]() ,
,![]() ,
,![]() ,所以数列2,
,所以数列2,![]() ,3的最佳值为
,3的最佳值为![]() .
.
小明进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的最佳值.如数列![]() ,2,3的最佳值为
,2,3的最佳值为![]() ;数列3,
;数列3,![]() ,2的最佳值为1;
,2的最佳值为1;![]() .经过研究,小明发现,对于“2,
.经过研究,小明发现,对于“2,![]() ,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为
,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)求数列![]() ,
,![]() ,2的最佳值;
,2的最佳值;
(2)将“![]() ,
,![]() ,1”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为 ,取得最佳值最小值的数列为 (写出一个即可);
,1”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为 ,取得最佳值最小值的数列为 (写出一个即可);
(3)将3,![]() ,
,![]() 这三个数按照不同的顺序排列,可得到若干个数列.若使数列的最佳值为1,求
这三个数按照不同的顺序排列,可得到若干个数列.若使数列的最佳值为1,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
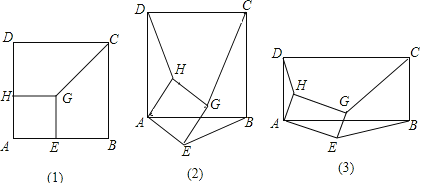
【题目】![]() 如图
如图![]() ,正方形AEGH的顶点E、H在正方形ABCD的边上,直接写出HD:GC:EB的结果______;
,正方形AEGH的顶点E、H在正方形ABCD的边上,直接写出HD:GC:EB的结果______;
![]() 将图
将图![]() 中的正方形AEGH绕点A旋转一定角度,如图
中的正方形AEGH绕点A旋转一定角度,如图![]() ,求HD:GC:EB;
,求HD:GC:EB;
![]() 把图
把图![]() 中的正方形都换成矩形,如图
中的正方形都换成矩形,如图![]() ,且已知DA:
,且已知DA:![]() :
:![]() ,求此时HD:GC:EB的值
,求此时HD:GC:EB的值![]() 简要写出过程
简要写出过程![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC=4,将△ABC△绕点A顺时针旋转60°,得到△ADE,连结BE,则BE的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com