
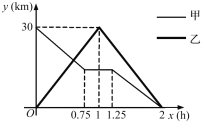
����Ŀ����һ����ֱ�Ĺ�·����A��B����.�ס�������ͬʱ����������綯����A������ǰ��B�أ����ߵ�һ��·��ʱ���ֹ��Ϻ�ͣ��ά��,�ó�����ԭ��������ʻ��B�أ�����Ħ�г���B������ǰ��A�أ�����A�غ�������ԭ·ԭ�����أ��������ͬʱ��B��.�ס���������B�صľ���y(km)������ʻʱ��x(h)֮��ĺ���ͼ����ͼ��ʾ.
��1�������ǰ���ٶ�.
��2����ס��ҵ�һ��������ʱ��.
��3��������֮��ľ��벻����10kmʱ���ܹ������߶Խ���������ϵ����ֱ��д�������н����������߶Խ�����ױ�����ϵ��xȡֵ��Χ.
���𰸡���1������ǰ���ٶ�Ϊ20km/h����2���ס��ҵ�һ���������ڳ�����0.6Сʱ����3��![]() ��
��![]() ��
��
��������
��1���ɺ���ͼ������������ʻ��ʱ�䣬�Ϳ�����·����ʱ���������ʻ���ٶȣ�
��2�������������������ϵֱ��������ۣ�
��3���������ǰy��x֮��ĺ�����ϵʽΪy��1��kx+b����������y��x֮��ĺ�����ϵʽΪy��2��k3x+b3����ǰ��A�صľ���y��km��������ʻʱ��x��h��֮��Ĺ�ϵʽΪy��1��k1x�����ҷ���B�ؾ���B�صľ���y��km��������ʻʱ��x��h��֮��Ĺ�ϵʽΪy��2��k2x+b2���ɴ���ϵ�����������ʽ��������ʽ�������⼴�ɣ�
��1�������⣬��
30��(2-![]() )=20��km/h����
)=20��km/h����
�����ǰ���ٶ�Ϊ20km/h��
��2���ɺ���ͼ��
��30+20��x��30��
���x��0.6��
��ס��ҵ�һ���������ڳ�����0.6Сʱ��
��3���������ǰy��x֮��ĺ�����ϵʽΪy��1��kx+b�������⣬��
![]() ��
��
��ã�![]() ��
��
y��1����20x+30��
���������y��x֮��ĺ�����ϵʽΪy��2��k3x+b3�������⣬��
 ��
��
��ã� ��
��
��y��2����20x+40��
����ǰ��A�صľ���y��km��������ʻʱ��x��h��֮��Ĺ�ϵʽΪy��1��k1x�������⣬��
30��k1��
��y��1��30x��
���ҷ���B�ؾ���B�صľ���y��km��������ʻʱ��x��h��֮��Ĺ�ϵʽΪy��2��k2x+b2�������⣬��
 ��
��
��ã� ��
��
��y����30x+60��
��![]() ʱ��
ʱ��
��![]() ��
��
![]() ��
��
��ã�![]() ��
��
��![]() ��
��![]() ��
��


 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д� ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�����о���ѧ����ʱ����һ�����壺�������Ѿ��ź�˳�������![]() ��
��![]() ��
��![]() ��������
��������![]() ��
��![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() ����������������Сֵ��Ϊ����
����������������Сֵ��Ϊ����![]() ��
��![]() ��
��![]() �����ֵ�����磬��������2��
�����ֵ�����磬��������2��![]() ��3����Ϊ
��3����Ϊ![]() ��
��![]() ��
��![]() ����������2��
����������2��![]() ��3�����ֵΪ
��3�����ֵΪ![]() ��
��
С����һ�����֣����ı�����������˳��ʱ�����õ������ж�����������������������Ӧ�����ֵ��������![]() ��2��3�����ֵΪ
��2��3�����ֵΪ![]() ������3��
������3��![]() ��2�����ֵΪ1��
��2�����ֵΪ1��![]() �������о���С�����֣�������2��
�������о���С�����֣�������2��![]() ��3���������������ղ�ͬ������˳��õ��IJ�ͬ�����У����ֵ����СֵΪ
��3���������������ղ�ͬ������˳��õ��IJ�ͬ�����У����ֵ����СֵΪ![]() ���������ϲ��ϣ��ش��������⣺
���������ϲ��ϣ��ش��������⣺
��1��������![]() ��
��![]() ��2�����ֵ��
��2�����ֵ��
��2������![]() ��
��![]() ��1�������������ղ�ͬ��˳�����У��ɵõ����ɸ����У���Щ���е����ֵ����СֵΪ�������� ��ȡ�����ֵ��Сֵ������Ϊ�������� ����д��һ�����ɣ���
��1�������������ղ�ͬ��˳�����У��ɵõ����ɸ����У���Щ���е����ֵ����СֵΪ�������� ��ȡ�����ֵ��Сֵ������Ϊ�������� ����д��һ�����ɣ���
��3����3��![]() ��
��![]() �����������ղ�ͬ��˳�����У��ɵõ����ɸ����У���ʹ���е����ֵΪ1����
�����������ղ�ͬ��˳�����У��ɵõ����ɸ����У���ʹ���е����ֵΪ1����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
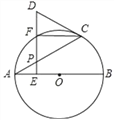
����Ŀ����ͼ��AB�ǡ�O��ֱ������P����AC��һ���㣨����A��C�غϣ�������P��PE��AB������ΪE������EP����AC�ڵ�F��������C�������ڵ�D��
��1����֤��DC��DP��
��2������CAB��30������F�ǻ�AC���е�ʱ���ж���A��O��C��FΪ������ı�����ʲô�����ı��Σ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
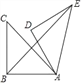
����Ŀ����ͼ����Rt��ABC�У���ABC=90����AB=BC=4������ABC���Ƶ�A˳ʱ����ת60�����õ���ADE������BE����BE�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ������������Σ���������֧Ԯƶ��ɽ��ѧУ�����мס�������ľ���飬����ÿ����������16�ף�����ÿ���������αȼ����8�ף����鵥����������Щ���α����鵥�����������20�죮ѧУÿ�츶����80Ԫ�����ѣ�������120Ԫ�����ѣ�
��1������ѧ�����������Σ�
��2�������������У�ѧУҪ��һ�����˽��������ල��ѧУ������ÿ��20Ԫ������ѣ�������������������
����һ���ɼ��鵥��������
�������������鵥��������
���������ס�������ͬʱ������
����Ϊ���ַ���ʡʱ��ʡǮ��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ������C��D�ǰ�ԲO�����ȷֵ㣬����C����O�����߽�AD���ӳ����ڵ�E������D��DF��AB�ڵ�F������O�ڵ�H������DC��AC��
��1����֤����AEC=90�㣻
��2�����ж��Ե�A��O��C��DΪ������ı��ε���״����˵�����ɣ�
��3����DC=2����DH�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=��x+4��ͼ���뷴��������y=![]() ��kΪ��������k��0����ͼ����A��1��a����B���㣮
��kΪ��������k��0����ͼ����A��1��a����B���㣮
��1�����������ı���ʽ����B�����ꣻ
��2����x������һ��P��ʹPA+PB��ֵ��С�������������ĵ�P�����꼰��PAB�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ����ݲ��ϻش�
����1��![]()
![]()
![]()
![]()
![]() .
.
����2��
8![]() ��0.125
��0.125![]() ��8��8��8��8��8��8��0.125��0.125��0.125��0.125��0.125��0.125
��8��8��8��8��8��8��0.125��0.125��0.125��0.125��0.125��0.125
��(8��0.125)��(8��0.125)��(8��0.125)��(8��0.125)��(8��0.125)��(8��0.125)
��(8��0.125)6 ��1.
��1������������ϵļ��㷽�����㣺![]() ��
��
��2��������ļ�����ܽ��һ�����ɣ�(����ĸ��ʾ) ![]() ��
��
��3���ã�2���Ĺ��ɼ��㣺![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
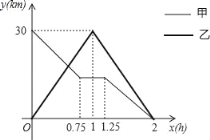
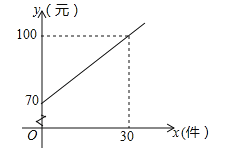
����Ŀ��ij��ݹ�˾��ÿλ�����С�硱��������ÿ�յ���������һ�κ�����ϵ����ͼ��ʾ��
��1����ÿλ�����С�硱��������y��Ԫ������������x������֮��ĺ�����ϵʽ��
��2����֪ij�����С�硱�������벻����110Ԫ����������Ҫ���Ͷ��ټ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com