
【题目】已知正比例函数![]() 的图象经过点(3,-6).
的图象经过点(3,-6).
(1)求这个函数的表达式;
(2)在如图所示的直角坐标系中画出这个函数的图象;
(3)判断点A(4,-2)、B(-1.5,3)是否在这个函数的图象上.
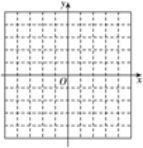
【答案】(1)![]() ;(2)画出图象如答图所示. 见解析;(3)点A(4,
;(2)画出图象如答图所示. 见解析;(3)点A(4,![]() )不在这个函数的图象上,点B(
)不在这个函数的图象上,点B(![]() ,3)在这个函数的图象上.
,3)在这个函数的图象上.
【解析】
(1)设出函数解析式y=kx,将点(3,-6)代入解析式即可得到k的值,从而求出函数解析式;
(2)根据解析式求出函数图象上的两个点即可画出函数图象;
(3)将点A(4,-2)、点B(-1.5,3)分别代入解析式,若等式成立,则点在函数图象上,否则,不在函数图象上
(1)把点(3,-6)代入正比例函数y=kx,得![]() ,解得
,解得![]() ,则函数的表达式为
,则函数的表达式为![]() .
.
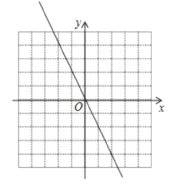
(2)函数![]() 经过点(0,0),(1,
经过点(0,0),(1,![]() ),画出图象如答图所示.
),画出图象如答图所示.
(3)∵正比例函数的表达式为![]() ,
,
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
∴点A(4,![]() )不在这个函数的图象上,点B(
)不在这个函数的图象上,点B(![]() ,3)在这个函数的图象上.
,3)在这个函数的图象上.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C,D是半圆O的三等分点,过点C作⊙O的切线交AD的延长线于点E,过点D作DF⊥AB于点F,交⊙O于点H,连接DC,AC.
(1)求证:∠AEC=90°;
(2)试判断以点A,O,C,D为顶点的四边形的形状,并说明理由;
(3)若DC=2,求DH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,△AB'C和△ABC关于AC所在的直线对称,AD和B'C相交于点O,连接BB'
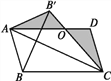
(1)请直接写出图中所有的等腰三角形(不添加字母);
(2)求证:△AB'O≌△CDO
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若△ABC中,其中一个内角是另一个内角的一半,则称△ABC为“半角三角形”.根据此定义,完成下面各题:
(1)若△ABC为半角三角形,且∠A=90°,则△ABC中其余两个角的度数为 ;
(2)若△ABC是半角三角形,且∠C=40°,则∠B ;
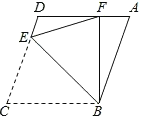
(3)如图,在四边形ABCD中,AB∥CD,AD∥BC,∠C=72°,点E在边CD上,以BE为折痕,将△BCE向上翻折,点C恰好落在AD边上的点F,若BF⊥AD,则△EDF是半角三角形吗?若是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
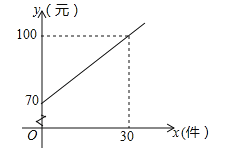
【题目】某快递公司的每位“快递小哥”日收入与每日的派送量成一次函数关系,如图所示.
(1)求每位“快递小哥”的日收入y(元)与日派送量x(件)之间的函数关系式;
(2)已知某“快递小哥”的日收入不少于110元,则他至少要派送多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【本小题满分9分】某校组织了一次初三科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品.C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图①和图②两幅尚不完整的统计图中.
(1)B班参赛作品有多少件?
(2)请你将图②的统计图补充完整;
(3)通过计算说明,哪个班的获奖率高?
(4)将写有A、B、C、D四个字母的完全相同的卡片放人箱中,从中一次随机抽出两张卡片,求抽到A、B两班的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() ,请探索给出数列的规律并解答下列问题:
,请探索给出数列的规律并解答下列问题:
(1)![]() ,
,![]() ,…,
,…,![]() ____________
____________
(2)观察下面的数表:
1
3 5
7 9 11 13
15 17 19 21 23 25 27 29
… …
设2019是该数表中的第![]() 行中的第
行中的第![]() 个数,求
个数,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2018春季环境整治活动中,某社区计划对面积为1600m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,若甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用5天.
(1)求甲、乙两工程队每天能完成绿化的面积;
(2)设甲工程队施工x天,乙工程队施工y天,刚好完成绿化任务,求y关于x的函数关系式;
(3)若甲队每天绿化费用是0.6万元,乙队每天绿化费用为0.25万元,且甲乙两队施工的总天数不超过25天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
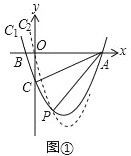
【题目】如图①,在平面直角坐标系中,抛物线C1:y=(x+k)(x﹣3)交x轴于点A、B(A在B的右侧),交y轴于点C,横坐标为2k的点P在抛物线C1上,连结PA、PC、AC,设△ACP的面积为S.
(1)求直线AC对应的函数表达式(用含k的式子表示).
(2)当点P在直线AC的下方时,求S取得最大值时抛物线C1所对应的函数表达式.
(3)当k取不同的值时,直线AC、抛物线C1和点P、点B都随k的变化而变化,但点P始终在不变的抛物线(虚线)C2:y=ax2+bx上,求抛物线C2所对应的函数表达式.
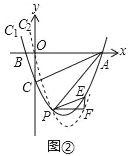
(4)如图②,当点P在直线AC的下方时,过点P作x轴的平行线交C2于点F,过点F作y轴的平行线交C1于点E,当△PEF与△ACO的相似比为![]() 时,直接写出k的值.
时,直接写出k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com