
【题目】如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=![]() (x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(1)求反比例函数和直线EF的解析式;
(2)求△OEF的面积;
(3)请结合图象直接写出不等式k2x+b﹣![]() >0的解集.
>0的解集.

【答案】(1)反比例函数解析式为y=![]() ;直线EF的解析式为y=﹣
;直线EF的解析式为y=﹣![]() x+5;(2)
x+5;(2)![]() ;(3)
;(3) ![]() .
.
【解析】试题分析:(1)先利用矩形的性质确定C点坐标(6,4),再确定A点坐标为(3,2),则根据反比例函数图象上点的坐标特征得到k1=6,即反比例函数解析式为y=![]() ;然后利用反比例函数解析式确定F点的坐标为(6,1),E点坐标为(
;然后利用反比例函数解析式确定F点的坐标为(6,1),E点坐标为(![]() ,4),再利用待定系数法求直线EF的解析式;
,4),再利用待定系数法求直线EF的解析式;
(2)利用△OEF的面积=S矩形BCDO-S△ODE-S△OBF-S△CEF进行计算;
(3)观察函数图象得到当![]() <x<6时,一次函数图象都在反比例函数图象上方,即k2x+b>
<x<6时,一次函数图象都在反比例函数图象上方,即k2x+b>![]() .
.
试题解析:(1)∵四边形DOBC是矩形,且D(0,4),B(6,0),
∴C点坐标为(6,4),
∵点A为线段OC的中点,
∴A点坐标为(3,2),
∴k1=3×2=6,
∴反比例函数解析式为y=![]() ;
;
把x=6代入y=![]() 得y=1,则F点的坐标为(6,1);
得y=1,则F点的坐标为(6,1);
把y=4代入y=![]() 得x=
得x=![]() ,则E点坐标为(
,则E点坐标为(![]() ,4),
,4),
把F(6,1)、E(![]() ,4)代入y=k2x+b得
,4)代入y=k2x+b得
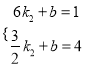 ,
,
解得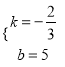 ,
,
∴直线EF的解析式为y=-![]() x+5;
x+5;
(2)△OEF的面积=S矩形BCDO-S△ODE-S△OBF-S△CEF
=4×6-![]() ×4×
×4×![]() -
-![]() ×6×1-
×6×1-![]() ×(6-
×(6-![]() )×(4-1)
)×(4-1)
=![]() ;
;
(3)由图象得:不等式k2x+b-![]() >0的解集为
>0的解集为![]() <x<6.
<x<6.


科目:初中数学 来源: 题型:
【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
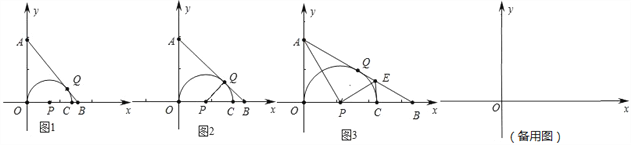
【题目】平面直角坐标系中,A(0,4),点P从原点O开始向x轴正方向运动,设P点横坐标为m,以点P为圆心,PO为半径作⊙P交x 轴另一点为C,过点A作⊙P的切线交 x轴于点B,切点为Q.
(1)如图1,当B点坐标为(3,0)时,求m;
(2)如图2,当△PQB为等腰三角形时,求m;
(3)如图3,连接AP,作PE⊥AP交AB于点E,连接CE,求证:CE是⊙P的切线;
(4)若在x轴上存在点M(8,0),在点P整个运动过程中,求MQ的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E。若DE=1,则BC的长为( )

A.2+![]() B.
B.![]() C.
C.![]() D.3
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,AD⊥DC,∠BAD=100°,在BC、CD上分别找一点M、N,当△AMN的周长最小时,∠AMN+∠ANM的度数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,对角线
中,对角线![]() 交于点
交于点![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.下列结论正确的是( )
的中点.下列结论正确的是( )
①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() 平分
平分![]() ;⑤四边形
;⑤四边形![]() 是菱形.
是菱形.
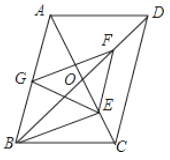
A.③⑤B.①②④C.①②③④D.①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是
是![]() 的外接圆,
的外接圆, ![]() 点在
点在![]() 边上,
边上, ![]() 的平分线交
的平分线交![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 的平行线,与
的平行线,与![]() 的延长线相交于点
的延长线相交于点![]() .
.
(1)求证: ![]() 是
是![]() 的切线;
的切线;
(2)求证:△PBD∽△DCA;
(3)当![]() 时,求线段
时,求线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数y=kx+5(x>-5)的图象G经过点A(-2,3),直线![]() 与图象G交于点B,与x轴交于点C.
与图象G交于点B,与x轴交于点C.
(1)求k的值;
(2)横、纵坐标都是整数的点叫做整点.记图象G在点A,B之间的部分与线段OA,OC,BC围成的区域(不含边界)为W.
①当b=2时,直接写出区域W内的整点个数;
②区域W内恰有3个整点,结合函数图象,求b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com