
【题目】如图,AB⊥BC,AD⊥DC,∠BAD=100°,在BC、CD上分别找一点M、N,当△AMN的周长最小时,∠AMN+∠ANM的度数是_____.

【答案】160°.
【解析】根据要使△AMN的周长最小,即利用点的对称,使三角形的三边在同一直线上,作出A关于BC和CD的对称点A′,A″,即可得出∠AA′M+∠A″=∠AA″A′=80°,进而得出∠AMN+∠ANM=2(∠AA′M+∠A″),即可得出答案.
作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.
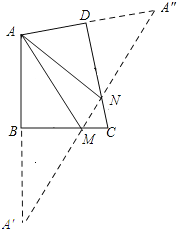
∵∠DAB=100°,
∴∠AA′M+∠A″=80°.
由轴对称图形的性质可知:∠MA′A=∠MAA′,∠NAD=∠A″,且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×80°=160°.
故答案为:160°.


科目:初中数学 来源: 题型:
【题目】关于频率与概率有下列几种说法:( )
①“明天下雨的概率是90%”表示明天下雨的可能性很大;
②“抛一枚硬币正面朝上的概率为![]() ”表示每抛两次就有一次正面朝上;
”表示每抛两次就有一次正面朝上;
③“某彩票中奖的概率是1%”表示买10张该种彩票不可能中奖;
④“抛一枚硬币正面朝上的概率为![]() ”表示随着抛掷次数的增加,“抛出正面朝上”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出正面朝上”这一事件发生的频率稳定在![]() 附近,正确的说法是
附近,正确的说法是
A.①④ B.②③ C.②④ D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)某校有学生2000名,为了了解学生在篮球、足球、排球和乒乓球这四项球类运动中最喜爱的一项球类运动情况,对学生开展了随机调查,丙将结果绘制成如下的统计图.

请根据以上信息,完成下列问题:
(1)本次调查的样本容量是 ;
(2)某位同学被抽中的概率是 ;
(3)据此估计全校最喜爱篮球运动的学生人数约有 名;
(4)将条形统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点M,O,N对应的数分别为﹣3,0,1,点P为数轴上任意一点,其对应的数为x.
(1)如果点P到点M、点N的距离相等,那么x的值是 ;
(2)当x= 时,使点P到点M、点N的距离之和是5;
(3)如果点P以每秒钟3个单位长度的速度从点O向左运动时,点M和点N分别以每秒钟1个单位长度和每秒钟4个单位长度的速度也向左运动,且三点同时出发,那么 秒钟时点P到点M,点N的距离相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.

情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:

你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市水费实行分段计费制,每户每月用水量在规定用量及以下的部分收费标准相同,超出规定用量的部分收费标准相同.例如:若规定用量为10吨,每月用水量不超过10吨按1.5元/吨收费,超出10吨的部分按2元/吨收费,则某户居民一个月用水8吨,则应缴水费:8×1.5=12(元);某户居民一个月用水13吨,则应缴水费:10×1.5+(13﹣10)×2=21(元).
表是小明家1至4月份用水量和缴纳水费情况,根据表格提供的数据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 6 | 7 | 12 | 15 |
水费(元) | 12 | 14 | 28 | 37 |
(1)该市规定用水量为 吨,规定用量内的收费标准是 元/吨,超过部分的收费标准是 元/吨.
(2)若小明家五月份用水20吨,则应缴水费 元.
(3)若小明家六月份应缴水费46元,则六月份他们家的用水量是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
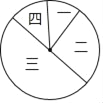
【题目】如图,一、二、三、四这四个扇形的面积之比为1:3:5:1.
(1)请分别求出它们圆心角的度数.
(2)一、二、四这三个扇形的圆心角的度数之和是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com