
【题目】下列方程中,解是x=﹣![]() 的是( )
的是( )
A. 3(x-![]() )=0 B. 2x﹣(x+1)=0 C.
)=0 B. 2x﹣(x+1)=0 C. ![]() D.
D. ![]()
【答案】C
【解析】
本题考查的是一元一次方程的解的定义,解决本题的方法可以采用代入验证求解,也可以分别求出已知方程的解进行判断,方程的解是指使方程左右两边相等的未知数的值。例如本题就是将x=﹣![]() 依次代入各个方程进行验证,从而得到本题的答案。
依次代入各个方程进行验证,从而得到本题的答案。
答案:C.
把x=﹣![]() 代入选项A. 3(x-
代入选项A. 3(x-![]() )=0,左边=3×(-
)=0,左边=3×(-![]() -
- ![]() )=3×(-1)=-3,右边=0,左边≠右边,所以x=﹣
)=3×(-1)=-3,右边=0,左边≠右边,所以x=﹣![]() 不是已知方程的解;
不是已知方程的解;
把x=﹣![]() 代入选项B. 2x﹣(x+1)=0,左边=2×(﹣
代入选项B. 2x﹣(x+1)=0,左边=2×(﹣![]() )-(﹣
)-(﹣![]() +1)=-1﹣
+1)=-1﹣![]() = -1
= -1![]() ,右边=0,左边≠右边,所以x=﹣
,右边=0,左边≠右边,所以x=﹣![]() 不是已知方程的解;
不是已知方程的解;
把x=﹣![]() 代入选项C.
代入选项C.![]() ,左边=(﹣
,左边=(﹣![]() – 1)×
– 1)×![]() =-
=-![]() ,右边= -
,右边= -![]() ,左边=右边,所以x=﹣
,左边=右边,所以x=﹣![]() 是已知方程的解;
是已知方程的解;
把x=﹣![]() 代入选项D.
代入选项D. ![]() ,左边=
,左边= ![]() ×(﹣
×(﹣![]() )= -
)= -![]() ,右边=0,左边≠右边,所以x=﹣
,右边=0,左边≠右边,所以x=﹣![]() 不是已知方程的解.
不是已知方程的解.
故选C.


科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G.点F是CD上一点,且满足 ![]() =
= ![]() ,连接AF并延长交⊙0于点E.连接AD,DE,若CF=2,AF=3.给出下列结论:
,连接AF并延长交⊙0于点E.连接AD,DE,若CF=2,AF=3.给出下列结论:
①△ADF∽△AED;②FG=2;③tan∠E= ![]() ;④S△DEF=4
;④S△DEF=4 ![]() .
.
其中正确的是( )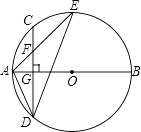
A.①②④
B.①②③
C.②③④
D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将45°的∠AOB按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数恰为2cm.若按相同的方式将37°的∠AOC放置在该刻度尺上,则OC与尺上沿的交点C在尺上的读数约为cm.(结果精确到0.1cm,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75) 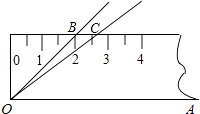
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由若干边长为1的小正方形拼成一系列“L”形图案(如图1).
(1)当“L”形由7个正方形组成时,其周长为;
(2)如图2,过格点D作直线EF,分别交AB,AC于点E,F.
①试说明AEAF=AE+AF;
②若“L”形由n个正方形组成时,EF将“L”形分割开,直线上方的面积为整个“L”形面积的一半,试求n的取值范围以及此时线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是初中数学的一个重要工具.利用数轴可以将数与形完美的结合.研究数轴我们发现了许多重要的规律:数轴上A点、B点表示的数为a、b,则A,B两点之间的距离AB=|a﹣b|,若a>b,则可简化为AB=a﹣b.
如图:
已知数轴上有A、B两点,分别表示的数为﹣10,8,点A以每秒3个单位的速度沿数轴向右匀速运动,点B以每秒2个单位向左匀速运动.设运动时间为t秒(t>0).
(综合运用).
(1)点A运动2秒后所在位置的点表示的数为 ;点B运动3秒后所在位置的点表示的数为 ;
(2)它们按上述方式运动,A、B两点经过多少秒会相遇,相遇点所表示的数是什么?
(3)它们按上述方式运动,A、B两点经过多少秒后相距2个单位长度?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E. 
(1)求证:△ABD≌△CAE;
(2)连接DE,线段DE与AB之间有怎样的位置和数量关系?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
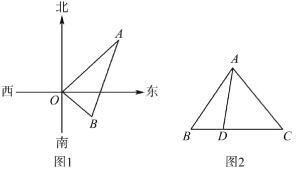
【题目】(1)如图1,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,求水管AB的长;
(2)如图2,在△ABC中,D是BC边上的点,已知AB=13,AD=12,AC=15,BD=5,求DC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com