
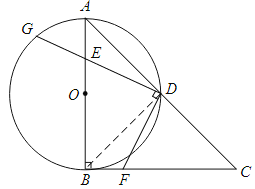
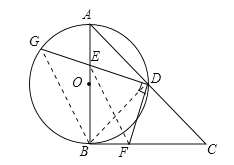
【题目】如图,在RtΔABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
(1)求证:AE=BF;
(2)连接EF,求证:∠FEB=∠GDA;
(3)连接GF,若AE=2,EB=4,求ΔGFD的面积.
【答案】(1)(2)见解析;(3)9
【解析】分析:(1)连接BD,由三角形ABC为等腰直角三角形,求出∠A与∠C的度数,根据AB为圆的直径,利用圆周角定理得到∠ADB为直角,即BD垂直于AC,利用直角三角形斜边上的中线等于斜边的一半,得到AD=DC=BD=![]() AC,进而确定出∠A=∠FBD,再利用同角的余角相等得到一对角相等,利用ASA得到三角形AED与三角形BFD全等,利用全等三角形对应边相等即可得证;
AC,进而确定出∠A=∠FBD,再利用同角的余角相等得到一对角相等,利用ASA得到三角形AED与三角形BFD全等,利用全等三角形对应边相等即可得证;
(2)连接EF,BG,由三角形AED与三角形BFD全等,得到ED=FD,进而得到三角形DEF为等腰直角三角形,利用圆周角定理及等腰直角三角形性质得到一对同位角相等,利用同位角相等两直线平行,再根据平行线的性质和同弧所对的圆周角相等,即可得出结论;
(3)由全等三角形对应边相等得到AE=BF=1,在直角三角形BEF中,利用勾股定理求出EF的长,利用锐角三角形函数定义求出DE的长,利用两对角相等的三角形相似得到三角形AED与三角形GEB相似,由相似得比例,求出GE的长,由GE+ED求出GD的长,根据三角形的面积公式计算即可.
详解:(1)连接BD.在Rt△ABC中,∠ABC=90°,AB=BC,∴∠A=∠C=45°.
∵AB为圆O的直径,∴∠ADB=90°,即BD⊥AC,∴AD=DC=BD=![]() AC,∠CBD=∠C=45°,∴∠A=∠FBD.
AC,∠CBD=∠C=45°,∴∠A=∠FBD.
∵DF⊥DG,∴∠FDG=90°,∴∠FDB+∠BDG=90°.
∵∠EDA+∠BDG=90°,∴∠EDA=∠FDB.在△AED和△BFD中,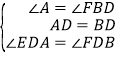 ,∴△AED≌△BFD(ASA),∴AE=BF;
,∴△AED≌△BFD(ASA),∴AE=BF;
(2)连接EF,BG.
∵△AED≌△BFD,∴DE=DF.
∵∠EDF=90°,∴△EDF是等腰直角三角形,∴∠DEF=45°.
∵∠G=∠A=45°,∴∠G=∠DEF,∴GB∥EF,∴∠FEB=∠GBA.
∵∠GBA=∠GDA,∴∠FEB=∠GDA;
(3)∵AE=BF,AE=2,∴BF=2.在Rt△EBF中,∠EBF=90°,∴根据勾股定理得:EF2=EB2+BF2.
∵EB=4,BF=2,∴EF=![]() =
=![]() .
.
∵△DEF为等腰直角三角形,∠EDF=90°,∴cos∠DEF=![]() .
.
∵EF=![]() ,∴DE=
,∴DE=![]() ×
×![]() =
=![]() .
.
∵∠G=∠A,∠GEB=∠AED,∴△GEB∽△AED,∴![]() =
=![]() ,即GEED=AEEB,∴
,即GEED=AEEB,∴![]() GE=8,即GE=
GE=8,即GE=![]() ,则GD=GE+ED=
,则GD=GE+ED=![]() .
.
∴![]() .
.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】某景区一电瓶小客车接到任务从景区大门出发,向东走2千米到达A景区,继续向东走2.5千米到达B景区,然后又回头向西走8.5千米到达C景区,最后回到景区大门.
![]()
(1)以景区大门为原点,向东为正方向,以1个单位长表示1千米,建立如图所示的数轴,请在数轴上表示出上述A、B、C三个景区的位置.
(2)A景区与C景区之间的距离是多少?
(3)若电瓶车充足一次电能行走15千米,则该电瓶车能否在一开始充足电而途中不充电的情况下完成此次任务?请计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的知识,后解答后面的问题:
探究:如图,在△ABC中,已知∠B=∠C,求证:AB=AC.

证明:过点A作AD⊥BC,垂足为D, 在△ABD与△ACD中,
∠B=∠C, , , 所以△ABD≌△ACD( ),所以AB=AC.
(1)完成上述证明中的空白;
(2)已知如图,在△ABC中,AC=BC,∠ACB=90°,AD平分∠CAB.试问:AC+CD与AB相等吗?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划选购甲、乙两种图书作为“校园读书节”的奖品.已知甲图书的单价是乙图书单价的![]() 倍;用
倍;用![]() 元单独购买甲种图书比单独购买乙种图书要少
元单独购买甲种图书比单独购买乙种图书要少![]() 本.
本.
(1)甲、乙两种图书的单价分别为多少元?
(2)若学校计划购买这两种图书共![]() 本,且投入的经费不超过
本,且投入的经费不超过![]() 元,要使购买的甲种图书数量不少于乙种图书的数量,则共有几种购买方案?
元,要使购买的甲种图书数量不少于乙种图书的数量,则共有几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
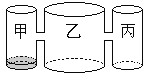
【题目】实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升![]() cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
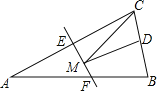
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为______.
周长的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=![]() ,点B的坐标为(m,-2).
,点B的坐标为(m,-2).
(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.

【答案】(1)△AHO的周长为12;(2) 反比例函数的解析式为y=![]() ,一次函数的解析式为y=-
,一次函数的解析式为y=-![]() x+1.
x+1.
【解析】试题分析: (1)根据正切函数,可得AH的长,根据勾股定理,可得AO的长,根据三角形的周长,可得答案;
(2)根据待定系数法,可得函数解析式.
试题解析:(1)由OH=3,tan∠AOH=![]() ,得
,得
AH=4.即A(-4,3).
由勾股定理,得
AO=![]() =5,
=5,
△AHO的周长=AO+AH+OH=3+4+5=12;
(2)将A点坐标代入y=![]() (k≠0),得
(k≠0),得
k=-4×3=-12,
反比例函数的解析式为y=![]() ;
;
当y=-2时,-2=![]() ,解得x=6,即B(6,-2).
,解得x=6,即B(6,-2).
将A、B点坐标代入y=ax+b,得
![]() ,
,
解得 ,
,
一次函数的解析式为y=-![]() x+1.
x+1.
考点:反比例函数与一次函数的交点问题.
【题型】解答题
【结束】
25
【题目】如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.
求证:①AB=AD;
②CD平分∠ACE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是等边三角形,点D、E分别在BC,AC且BD=CE,AD、BE相交于点M,

求证:(1)△AME∽△BAE;(2)BD2=AD×DM.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com