【题目】若关于x的方程mx＝2﹣x的解为整数，且m为负整数，求代数式5m2﹣[m2﹣（6m﹣5m2）﹣2（m2﹣3m）]的值．
【答案】m2，4或9．
【解析】
先求出方程的解，根据方程的解为整数且m为负整数求出m的值，再化简代数式，最后代入求值即可．
解：解方程mx＝2﹣x
得：x＝
，
∵关于x的方程mx＝2﹣x的解为整数，
∴1+m＝±2或±1，
解得：m＝1或﹣3或0或﹣2，
∵m为负整数，
∴m＝1和m＝0舍去（不是负整数），
即m＝﹣3或﹣2；
5m2﹣[m2﹣（6m﹣5m2）﹣2（m2﹣3m）]
＝5m2﹣[m2﹣6m+5m2﹣2m2+6m]
＝5m2﹣m2+6m﹣5m2+2m2﹣6m
＝m2，
当m＝﹣2时，原式＝（﹣2）2＝4；
当m＝﹣3时，原式＝（﹣3）2＝9，
所以代数式5m2﹣[m2﹣（6m﹣5m2）﹣2（m2﹣3m）]的值是4或9．
科目：初中数学 来源： 题型：
【题目】点
，
在数轴上分别表示有理数
，
，，两点之间的距离表示为
，在数轴上，两点之间的距离
.已知数轴上，两点表示数，满足
，点
为数轴上一动点，其对应的数为
.
（1），两点之间的距离是.
（2）与
之间的距离表示为.
（3）数轴上是否存在点，使点到点，点的距离之和为
？若存在，请求出的值；若不存在，说明理由.
（4）现在点，点分别以
单位/秒和
单位/秒的速度同时向右运动，当点与点之间的距离为
个单位长度时，求点所对应的数是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】菱形ABCD中，∠B＝60°，点E在边BC上，点F在边CD上．
(1)如图①，若点E是BC的中点，∠AEF＝60°，求证：BE＝DF；
(2)如图②，若∠EAF＝60°，求证：△AEF是等边三角形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下面一列数，探究其中的规律：—1，
，
，
，
，
（1）填空：第11，12，13三个数分别是 ， ， ；
（2）第2020个数是什么？
（3）如果这列数无限排列下去，与哪个数越来越近？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】夏师傅是一名徒步运动的爱好者，他用手机软件记录了某个月（30天）每天徒步的步数（单位：万步），将记录结果绘制成了如图所示的统计图．在这组徒步数据中，众数和中位数分别是（ ）
A. 1.2，1.3 B. 1.4，1.3 C. 1.4，1.35 D. 1.3，1.3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线y＝－x2＋2x＋3与x轴交于点A、B(点A在点B的左侧)，与y轴交于点C.
(1)求直线BC的表达式；
(2)抛物线的对称轴上存在点P，使∠APB＝∠ABC，利用图①求点P的坐标；
(3)点Q在y轴右侧的抛物线上，利用图②比较∠OCQ与∠OCA的大小，并说明理由．
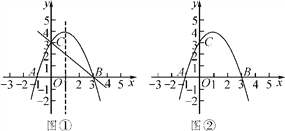
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，P为边长为2的等边三角形ABC内任意一点，连接PA、PB、PC，过P点分别作BC、AC、AB边的垂线，垂足分别为D、E、F，则PD+PE+PF等于（ ）
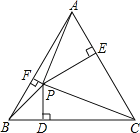
A.
B.
C.2D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在RtΔABC中，∠ABC=90°，AB=CB，以AB为直径的⊙O交AC于点D，点E是AB边上一点（点E不与点A、B重合），DE的延长线交⊙O于点G，DF⊥DG，且交BC于点F.
（1）求证：AE=BF；
（2）连接EF，求证：∠FEB=∠GDA；
（3）连接GF,若AE=2，EB=4，求ΔGFD的面积.
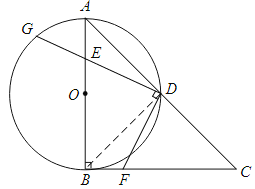
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】右图为手的示意图，在各个手指之间标记字母A，B，C，D。请你按图中箭头所指的方向（即A→B→C→D→C→B→A→B→C→……的方式）从A开始数连续的正整数1，2,3,4,5,6,7,8,9，……
（1）当数到14时，对应的字母是_________；
（2）当字母C第201次出现时。恰好数到的数是_________；
（3）当字母C第2n+1次出现时（n为正整数），恰好数到的数是__________（用含有n的代数式表示）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com