
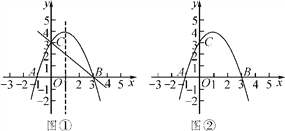
【题目】抛物线y=-x2+2x+3与x轴交于点A、B(点A在点B的左侧),与y轴交于点C.
(1)求直线BC的表达式;
(2)抛物线的对称轴上存在点P,使∠APB=∠ABC,利用图①求点P的坐标;
(3)点Q在y轴右侧的抛物线上,利用图②比较∠OCQ与∠OCA的大小,并说明理由.
【答案】(1)y=-x+3(2)P点的坐标为(1,2+2![]() )或(1,-2-2
)或(1,-2-2![]() )(3)当Q点的横坐标为5时,∠OCA=∠OCQ;当Q点的横坐标大于5时,则∠OCQ逐渐变小,故∠OCA>∠OCQ;当Q点的横坐标小于5且大于0时,则∠OCQ逐渐变大,故∠OCA<∠OCQ.
)(3)当Q点的横坐标为5时,∠OCA=∠OCQ;当Q点的横坐标大于5时,则∠OCQ逐渐变小,故∠OCA>∠OCQ;当Q点的横坐标小于5且大于0时,则∠OCQ逐渐变大,故∠OCA<∠OCQ.
【解析】试题分析:(1)由抛物线解析式可求B、C的坐标,利用待定系数法可求直线BC的解析式;
(2)由直线BC的解析式可知∠APB=∠ABC=45°,设抛物线对称轴交直线BC于点D,交x轴于点E,结合二次函数的对称性可得PB=PD,根据勾股定理求出BD的长,从而求出PE的长,进而求出P的坐标;
(3)设Q(x,-x2+2x+3),当∠OCA=∠OCQ时,利用三角形相似可得到关于x的方程,求出Q点的横坐标,再结合图形比较两角的大小.
试题解析:(1)在y=-x2+2x+3中,令y=0可得0=-x2+2x+3,解得x=-1或x=3,令x=0可得y=3,∴B(3,0),C(0,3).∴可设直线BC的表达式为y=kx+3,把B点坐标代入可得3k+3=0,解得k=-1,∴直线BC的表达式为y=-x+3.
(2)∵OB=OC,∴∠ABC=45°.∵y=-x2+2x+3=-(x-1)2+4,∴抛物线的对称轴为直线x=1.
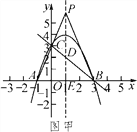
设抛物线的对称轴交直线BC于点D,交x轴于点E,当点P在x轴上方时,如图甲,∵∠APB=∠ABC=45°,且PA=PB,∴∠PBA=67.5°,∠DPB=![]() ∠APB=22.5°,∴∠PBD=22.5°,∴∠DPB=∠DBP,∴DP=DB.在Rt△BDE中,BE=DE=2,∴BD=2
∠APB=22.5°,∴∠PBD=22.5°,∴∠DPB=∠DBP,∴DP=DB.在Rt△BDE中,BE=DE=2,∴BD=2![]() ,∴PE=2+2
,∴PE=2+2![]() ,∴P(1,2+2
,∴P(1,2+2![]() );
);
当点P在x轴下方时,由对称性可知P点坐标为(1,-2-2![]() ).
).
综上可知,P点的坐标为(1,2+2![]() )或(1,-2-2
)或(1,-2-2![]() ).
).
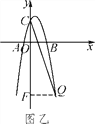
(3)设Q(x,-x2+2x+3),当点Q在x轴下方时,如图乙,过点Q作QF⊥y轴于点F,则CF=x2-2x.当∠OCA=∠OCQ时,则△QFC∽△AOC,∴![]() ,即
,即![]() ,解得x=0(舍去)或x=5.
,解得x=0(舍去)或x=5.
∴当Q点的横坐标为5时,∠OCA=∠OCQ;当Q点的横坐标大于5时,则∠OCQ逐渐变小,故∠OCA>∠OCQ;当Q点的横坐标小于5且大于0时,则∠OCQ逐渐变大,故∠OCA<∠OCQ.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
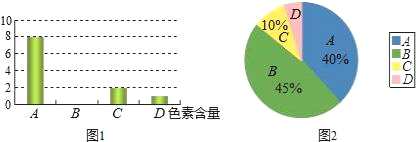
【题目】为了调查市场上某品牌方便面的色素含量是否符合国家标准,工作人员在超市里随机抽取了某品牌的方便面进行检验.图1和图2是根据调查结果绘制的两幅不完整的统计图,其中A、B、C、D分别代表色素含量为0.05%以下、0.05%~0.1%、0.1%~0.15%、0.15%以上,图1的条形图表示的是抽查的方便面中色素含量分布的袋数,图2的扇形图表示的是抽查的方便面中色素的各种含量占抽查总数的百分比.请解答以下问题:
(1)本次调查一共抽查了多少袋方便面?
(2)将图1中色素含量为B的部分补充完整;
(3)图2中的色素含量为D的方便面所占的百分比是多少?
(4)若色素含量超过0.15%即为不合格产品,某超市这种品牌的方便面共有10000袋,那么其中不合格的产品有多少袋?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形![]() 中,点
中,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,把
,把![]() 沿
沿![]() 折叠得到
折叠得到![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
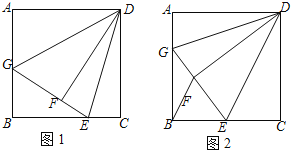
(1)求![]() 的度数.
的度数.
(2)如图![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
①求证:![]() ;
;
②若正方形边长为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为3的正方形OABC的两边在两坐标轴上,抛物线y=-x2+bx+c经过点A,C,与x轴交于另一点D,P为第一象限内抛物线上一点,过P点作y轴的平行线交x 轴于点Q,交AC于点E.
(1)求抛物线解析式及点D的坐标;
(2)过E点作x轴的平行线交AB于点F,若以P,E,F为顶点的三角形与△ODC相似,求点P坐标;
(3)过P点作PH⊥AC于H,是否存在点P使△PEH的周长取得最大值,若存在,请求出点P坐标及△PEH周长的最大值,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB,AC边的垂直平分线分别交BC于点D,E,垂足分别为点F,G,△ADE的周长为6cm.
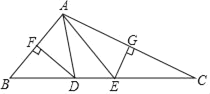
(1)求△ABC中BC边的长度;
(2)若∠BAC=116°,求∠DAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的知识,后解答后面的问题:
探究:如图,在△ABC中,已知∠B=∠C,求证:AB=AC.

证明:过点A作AD⊥BC,垂足为D, 在△ABD与△ACD中,
∠B=∠C, , , 所以△ABD≌△ACD( ),所以AB=AC.
(1)完成上述证明中的空白;
(2)已知如图,在△ABC中,AC=BC,∠ACB=90°,AD平分∠CAB.试问:AC+CD与AB相等吗?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升![]() cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
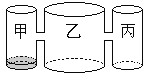
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l:y=﹣x+4分别与x轴、y轴交于点A,B,双曲线![]() (k>0,x>0)与直线l不相交,E为双曲线上一动点,过点E作EG⊥x轴于点G,EF⊥y轴于点F,分别与直线l交于点C,D,且∠COD=45°,则k=_____.
(k>0,x>0)与直线l不相交,E为双曲线上一动点,过点E作EG⊥x轴于点G,EF⊥y轴于点F,分别与直线l交于点C,D,且∠COD=45°,则k=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com