
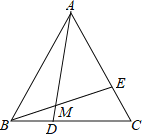
【题目】已知:如图,△ABC是等边三角形,点D、E分别在BC,AC且BD=CE,AD、BE相交于点M,

求证:(1)△AME∽△BAE;(2)BD2=AD×DM.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据等边三角形的性质可得出AB=BC、∠ABD=∠C,结合BD=CE即可证出△ABD≌△BCE(SAS),根据全等三角形的性质可得出∠CBE=∠BAD,通过角的计算可得出∠EAM=∠EBA,再结合∠AEM=∠BEA即可证出△AME∽△BAE;
(2)根据相似三角形的性质可得出∠AME=∠BAE=60°,由对顶角相等可得出∠BMD=60°,再结合∠ABD=60°、∠BDM=∠ADB,即可证出△ABD∽△BMD,根据相似三角形的性质可证出BD2=AD×DM.
证明:(1)∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠C=60°.
在△ABD和△BCE中, ,
,
∴△ABD≌△BCE(SAS),
∴∠CBE=∠BAD,
∴∠EAM=∠EBA.
又∵∠AEM=∠BEA,
∴△AME∽△BAE.
(2)∵△AME∽△BAE,
∴∠AME=∠BAE=60°,
∴∠BMD=60°.
又∵∠ABD=60°,∠BDM=∠ADB,
∴△ABD∽△BMD,
∴BD2=AD×DM.


科目:初中数学 来源: 题型:
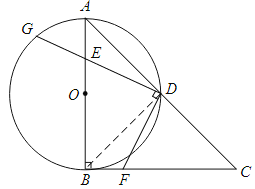
【题目】如图,在RtΔABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
(1)求证:AE=BF;
(2)连接EF,求证:∠FEB=∠GDA;
(3)连接GF,若AE=2,EB=4,求ΔGFD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】右图为手的示意图,在各个手指之间标记字母A,B,C,D。请你按图中箭头所指的方向(即A→B→C→D→C→B→A→B→C→……的方式)从A开始数连续的正整数1,2,3,4,5,6,7,8,9,……

(1)当数到14时,对应的字母是_________;
(2)当字母C第201次出现时。恰好数到的数是_________;
(3)当字母C第2n+1次出现时(n为正整数),恰好数到的数是__________(用含有n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠AOB和两点C、D,求作一点P,使PC=PD,且点P到∠AOB的两边的距离相等.
(要求:用尺规作图,保留作图痕迹,写出作法,不要求证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,梯形ABCD中,AD∥BC,∠C=90°,BA=BC.动点E、F同时从点B出发,点E沿折线 BA–AD–DC运动到点C时停止运动,点F沿BC运动到点C时停止运动,它们运动时的速度都是1 cm/s.设E出发t s时,△EBF的面积为y cm2.已知y与t的函数图象如图②所示,其中曲线OM为抛物线的一部分,MN、NP为线段.
请根据图中的信息,解答下列问题:
(1)AD= cm,BC= cm;
(2)求a的值,并用文字说明点N所表示的实际意义;
(3)直接写出当自变量t为何值时,函数y的值等于5.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,AC=2![]() .
.
(1)利用尺规作线段AC的垂直平分线DE,垂足为E,交AB于点D;(保留作图痕迹,不写作法)
(2)若△ADE的周长为a,先化简T=(a+1)2﹣a(a﹣1),再求T的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,A、B分别为数轴上的两点,A点对应的数为-20,B点对应的数为100.
![]()
请写出AB中点M对应的数。
(2)现有一只电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动。设两只电子蚂蚁在数轴上的C点相遇,你知道C点对应的数是多少吗?
(3)若当电子蚂蚁P从B点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度也向左运动。设两只电子蚂蚁在数轴上的D点相遇,你知道D点对应的数是多少吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=![]() ,tanB=
,tanB=![]() .半径为2的⊙C, 分别交AC、BC于点D、E,得到
.半径为2的⊙C, 分别交AC、BC于点D、E,得到![]() .
.
(1)求证:AB为⊙C的切线;
(2)求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自学下面材料后,解答问题.
分母中含有未知数的不等式叫分式不等式.如:![]() ;
;![]() 等.那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:
等.那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:
(1)若![]() >0,
>0,![]() >0,则
>0,则![]() >0;若
>0;若![]() <0,
<0,![]() <0,则
<0,则![]() >0;
>0;
(2)若![]() >0,
>0,![]() <0,则
<0,则![]() <0;若
<0;若![]() <0,
<0,![]() >0,则
>0,则![]() <0.
<0.
反之:(1)若![]() >0,则
>0,则![]() 或
或![]()
(2)若![]() <0,则__________或__________.
<0,则__________或__________.
(3)根据上述规律,求不等式![]() 的解集.
的解集.
(4)试求不等式![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com