
【题目】如图,Rt△ABC中,∠C=90°,AC=![]() ,tanB=
,tanB=![]() .半径为2的⊙C, 分别交AC、BC于点D、E,得到
.半径为2的⊙C, 分别交AC、BC于点D、E,得到![]() .
.
(1)求证:AB为⊙C的切线;
(2)求图中阴影部分的面积.

【答案】(1)证明见解析(2)5-π
【解析】分析:(1)过点C作CF⊥AB于点F。根据三角函数的计算公式和勾股定理可得BC、AB的长,根据三角形的面积公式可求得CF的长,因为CF的长等于圆的半径长,利用切线的判定即可证明。(2)根据三角形的面积公式、扇形的面积公式以及阴影部分的面积等于△ABC的面积与扇形DCE的面积之差,即可求得阴影部分的面积.
详解:(1)证明:过C作CF⊥AB于F,
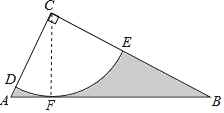
∵在Rt△ABC中,∠C=90°,AC=![]() ,tanB=
,tanB=![]() =
=![]() ,
,
∴BC=2![]() ,
,
由勾股定理得:AB=![]() =5,
=5,
∵△ACB的面积S=![]() =
=![]() ,
,
∴CF=![]() =2,
=2,
∴CF为⊙C的半径,
∵CF⊥AB,
∴AB为⊙C的切线;
(2)解:图中阴影部分的面积=S△ACB﹣S扇形DCE=![]() ×
×![]() ×2
×2![]() ﹣
﹣![]() =5﹣π.
=5﹣π.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=![]() ,点B的坐标为(m,-2).
,点B的坐标为(m,-2).
(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.

【答案】(1)△AHO的周长为12;(2) 反比例函数的解析式为y=![]() ,一次函数的解析式为y=-
,一次函数的解析式为y=-![]() x+1.
x+1.
【解析】试题分析: (1)根据正切函数,可得AH的长,根据勾股定理,可得AO的长,根据三角形的周长,可得答案;
(2)根据待定系数法,可得函数解析式.
试题解析:(1)由OH=3,tan∠AOH=![]() ,得
,得
AH=4.即A(-4,3).
由勾股定理,得
AO=![]() =5,
=5,
△AHO的周长=AO+AH+OH=3+4+5=12;
(2)将A点坐标代入y=![]() (k≠0),得
(k≠0),得
k=-4×3=-12,
反比例函数的解析式为y=![]() ;
;
当y=-2时,-2=![]() ,解得x=6,即B(6,-2).
,解得x=6,即B(6,-2).
将A、B点坐标代入y=ax+b,得
![]() ,
,
解得 ,
,
一次函数的解析式为y=-![]() x+1.
x+1.
考点:反比例函数与一次函数的交点问题.
【题型】解答题
【结束】
25
【题目】如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.
求证:①AB=AD;
②CD平分∠ACE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是等边三角形,点D、E分别在BC,AC且BD=CE,AD、BE相交于点M,

求证:(1)△AME∽△BAE;(2)BD2=AD×DM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠![]() =90°,
=90°,![]() =
=![]() =6,点
=6,点![]() 在边
在边![]() 上运动,过点
上运动,过点![]() 作
作![]() ⊥
⊥![]() 于点
于点![]() ,以
,以![]() 、
、![]() 为邻边作□
为邻边作□![]() ,设□
,设□![]() 与△
与△![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,线段
,线段![]() 的长为
的长为![]() (0<
(0<![]() ≤6).
≤6).
(1)求线段![]() 的长(用含
的长(用含![]() 的代数式表示)
的代数式表示)
(2)当点![]() 落现在变
落现在变![]() 上时,求
上时,求![]() 的值;
的值;
(3)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(4)直接写出点![]() 到△
到△![]() 任意两边所在直线的距离相等时
任意两边所在直线的距离相等时![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,列一元一次方程解应用题,回答下列问题:
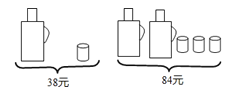
(1)求一个暖瓶与一个水杯分别是多少元?
(2)若买3个暖瓶与4个水杯一共需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划购买若干台电脑,现从两家商场了解到同一种型号的电脑报价均为6000元,并且多买都有一定的优惠.各商场的优惠条件如下表所示:
商场 | 优惠条件 |
甲商场 | 第一台按原价收费,其余的每台优惠25% |
乙商场 | 每台优惠20% |
(1)设学校购买![]() 台电脑,选择甲商场时,所需费用为
台电脑,选择甲商场时,所需费用为![]() 元,选择乙商场时,所需费用为
元,选择乙商场时,所需费用为![]() 元,请分别求出
元,请分别求出![]() ,
,![]() 与
与![]() 之间的关系式.
之间的关系式.
(2)什么情况下,两家商场的收费相同?什么情况下,到甲商场购买更优惠?什么情况下,到乙商场购买更优惠?
(3)现在因为急需,计划从甲乙两商场一共买入10台电脑,已知甲商场的运费为每台50元,乙商场的运费为每台60元,设总运费为![]() 元,从甲商场购买
元,从甲商场购买![]() 台电脑,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?
台电脑,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对
他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
(计算方差的公式:s2=![]() [
[![]() ])
])
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,AB⊥AC,点E是BC的中点,AE与BD交于点F,且F是AE的中点.
(Ⅰ)求证:四边形AECD是菱形;(Ⅱ)若AC=4,AB=5,求四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点0为直线AB上一点,∠AOC=50![]() ,OD平分∠AOC,∠DOE=90
,OD平分∠AOC,∠DOE=90![]() .
.
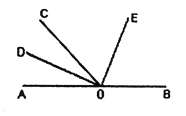
(1)请你数一数,图中有多少个小于平角的角:
(2)求出∠BOD的度数;
(3)试判断OE是否平分∠BOC,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com