
【题目】如图,在△ABC中,∠![]() =90°,
=90°,![]() =
=![]() =6,点
=6,点![]() 在边
在边![]() 上运动,过点
上运动,过点![]() 作
作![]() ⊥
⊥![]() 于点
于点![]() ,以
,以![]() 、
、![]() 为邻边作□
为邻边作□![]() ,设□
,设□![]() 与△
与△![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,线段
,线段![]() 的长为
的长为![]() (0<
(0<![]() ≤6).
≤6).
(1)求线段![]() 的长(用含
的长(用含![]() 的代数式表示)
的代数式表示)
(2)当点![]() 落现在变
落现在变![]() 上时,求
上时,求![]() 的值;
的值;
(3)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(4)直接写出点![]() 到△
到△![]() 任意两边所在直线的距离相等时
任意两边所在直线的距离相等时![]() 的值.
的值.

【答案】(1)![]() x;(2)x=4;(3)
x;(2)x=4;(3)![]() 或
或![]() ;(4)3,6,
;(4)3,6,  .
.
【解析】试题分析:(1)利用平行四边形和三角函数值,可求出PE长.(2)利用三角函数把AP,PC用x表示出来,求值.(3)AP的长度分类讨论,可求得两个二次函数解析式.(4)求E到各边的距离,直接写出结果.
试题解析:
(1)∠C=90°,AB=AC,∴∠A=45°,
∵PD![]() AB,∴AD=APcos∠A=
AB,∴AD=APcos∠A=![]() x=PD,
x=PD,
∵四边形PADE是平行四边形,
PE=AD=![]() x.
x.
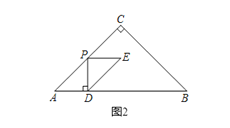
(2)当E点落在BC上,图1,PE![]() AD,∴∠CPE=45°,
AD,∴∠CPE=45°,
∴PC=PEcos∠CPE=![]() x
x![]() =
=![]() ,
,
所以AP+PC=AC,
所以x+![]() =6, x=4.
=6, x=4.
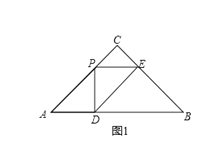
(3)当0<x![]() 时,y=AD
时,y=AD![]() .图2,
.图2,
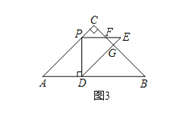
当4<x![]() 6,设DE与 BC交于G,PE与BC交于F,图3,
6,设DE与 BC交于G,PE与BC交于F,图3,
AD=![]() x,AB=
x,AB=![]() AC=6
AC=6![]() ,
,
∴DB=AB![]() AD=6
AD=6![]() -
-![]() x,
x,
∴DG=DBsin∠B=6-![]() ,
,
∴GE=DE-DG=![]() ,
,
y=S四边形PADE-S△GFE=![]() 2
2
= ![]() .
.
(4)3,6, 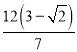 .
.


科目:初中数学 来源: 题型:
【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠AOB和两点C、D,求作一点P,使PC=PD,且点P到∠AOB的两边的距离相等.
(要求:用尺规作图,保留作图痕迹,写出作法,不要求证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,AC=2![]() .
.
(1)利用尺规作线段AC的垂直平分线DE,垂足为E,交AB于点D;(保留作图痕迹,不写作法)
(2)若△ADE的周长为a,先化简T=(a+1)2﹣a(a﹣1),再求T的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,A、B分别为数轴上的两点,A点对应的数为-20,B点对应的数为100.
![]()
请写出AB中点M对应的数。
(2)现有一只电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动。设两只电子蚂蚁在数轴上的C点相遇,你知道C点对应的数是多少吗?
(3)若当电子蚂蚁P从B点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度也向左运动。设两只电子蚂蚁在数轴上的D点相遇,你知道D点对应的数是多少吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有4张正面分别标有数字﹣1,2,﹣3,4的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上,洗匀后从4张卡片中随机摸出一张不放回,将该卡片上的数字记为m,在随机抽取1张,将卡片的数字即为n.
(1)请用列表或树状图的方式把(m,n)所有的结果表示出来.
(2)求选出的(m,n)在二、四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=![]() ,tanB=
,tanB=![]() .半径为2的⊙C, 分别交AC、BC于点D、E,得到
.半径为2的⊙C, 分别交AC、BC于点D、E,得到![]() .
.
(1)求证:AB为⊙C的切线;
(2)求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一列数:1,―2,3,―4,5,―6,7,… 将这列数排成下列形式:
第1行 1
第2行 -2 3
第3行 -4 5 -6
第4行 7 -8 9 -10
第5行 11 -12 13 -14 15
… …
按照上述规律排下去,那么第10行从左边数第5个数等于
A.50B.-50C.60D.-60
查看答案和解析>>
科目:初中数学 来源: 题型:
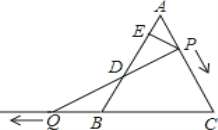
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)证明:在运动过程中,点D是线段PQ的中点;
(3)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com