
【题目】已知:如图,∠EOF=60°,在射线OE上取一点A,使OA=10cm,在射线OF上取一点B,使OB=16cm.以OA、OB为邻边作平行四边形OACB.若点P在射线OF上,点Q在线段CA上,且CQ:OP=1:2.设CQ=a(a>0).

(1)连接PQ,当a=2时,求线段PQ的长度.
(2)若以点P、B、C、Q四点为顶点的四边形是平行四边形时,求a的值.
(3)连接PQ,以PQ所在的直线为对称轴,作点C关于直线PQ的对称点C',当点C′恰好落在平行四边形OACB的边上或者边所在的直线上时,直接写出a的值.
【答案】(1)![]() ;(2)
;(2)![]() 或16;(3)7或14-2
或16;(3)7或14-2![]() 或12.
或12.
【解析】
(1)如图1,作辅助线,构建直角三角形,计算PM和MQ的长,利用勾股定理可得PQ的长;
(2)分两种情况:
①当P在边OB上时,如图2,四边形PBCQ是平行四边形,
②当P在OB的延长线上时,如图3,四边形BPCQ是平行四边形,
分别根据PB=CQ列方程可得结论;
(3)存在三种情况:①如图4,当C'在边AC上时,PQ⊥AC,过B作BD⊥AC于D时,则BD∥PQ,
②如图5,当C'在边OB上时,连接PC、CC'、C'Q,过C作CR⊥OP于R,
③如图6,当C'在直线CB上时,连接PC、CC'、C'Q,
分别根据对称性和直角三角形的性质列方程可得结论.
解:(1)如图1,过A作AN⊥OB于N,过B作BD⊥AC于D,过Q作QM⊥OF于M,则AN∥BD∥MQ,
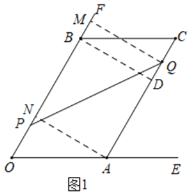
Rt△AON中,∠AOB=∠EOF=60°,OA=10,
∴ON=![]() OA=5,AN=5
OA=5,AN=5![]() ,
,
同理得:CD=5,BD=5![]() ,
,
∵四边形OACB是平行四边形,
∴OB∥AC,
∴MQ=BD=5![]() ,
,
当a=2时,CQ=2,OP=4,
∴BM=DQ=5-2=3,
∴PM=PB+BM=16-4+3=15,
Rt△PMQ中,由勾股定理得:PQ=![]() =
=![]() =10
=10![]() (cm);
(cm);
(2)分两种情况:
①当P在边OB上时,如图2,四边形PBCQ是平行四边形,
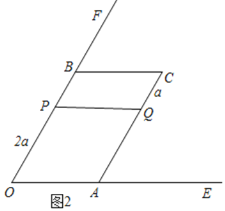
∴PB=CQ,
即16-2a=a,
a=![]() ;
;
②当P在OB的延长线上时,如图3,四边形BPCQ是平行四边形,
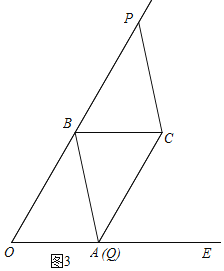
∴PB=CQ
即2a-16=a,
a=16,此时Q与A重合,
综上,a的值为![]() 或16;
或16;
(3)分三种情况:
①如图4,当C'在边AC上时,PQ⊥AC,过B作BD⊥AC于D时,则BD∥PQ,
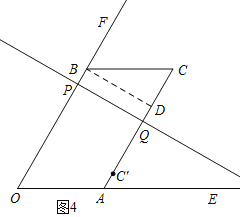
∴PB=QD,
16-2a=a-5,
3a=21,
a=7;
②如图5,当C'在边OB上时,连接PC、CC'、C'Q,过C作CR⊥OP于R,

∵C与C'关于PQ对称,
∴PQ是CC'的垂直平分线,
∴PC=PC',CQ=C'Q,
∴∠PCC'=∠PC'C,
∵AC∥OP,
∴∠PC'C=∠QCC',
∴∠QCC'=∠PCC',
∵CC'⊥PQ,
∴PC=CQ=a,
∵OP=2a,
∴BP=2a-16,
Rt△BCR中,∠CBR=60°,
∴∠BCR=30°,
∵BC=10,
∴BR=5,CR=5![]() ,
,
∴PR=5-(2a-16)=21-2a,
由勾股定理得:![]() ,
,
a=14+2![]() (舍)或14-2
(舍)或14-2![]() ;
;
③如图6,当C'在直线CB上时,连接PC、PC'、C'Q,
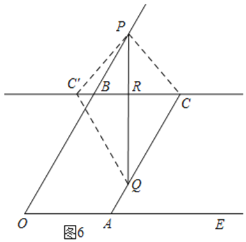
Rt△PBR中,∠PBR=60°,
∴∠BPR=30°,
∵PB=2a-16,
∴BR=![]() BP=a-8,
BP=a-8,
同理得:CR=![]() CQ=
CQ=![]() a,
a,
∵BC=BR+CR,
∴a-8+![]() a=10,a=12,
a=10,a=12,
综上,a的值为7或14-2![]() 或12.
或12.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H交BE于G.下列结论:①BD=CD;②AD+CF=BD;③CE=![]() BF;④AE=BG.其中正确的个数是( )
BF;④AE=BG.其中正确的个数是( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)8a+7b+2c>0;(3)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;(4)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有().
,y3)在该函数图象上,则y1<y3<y2;(4)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有().
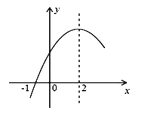
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 为AC边中点,动点
为AC边中点,动点![]() 从点
从点![]() 出发,沿着
出发,沿着![]() 的路径以每秒1个单位长度的速度运动到
的路径以每秒1个单位长度的速度运动到![]() 点,在此过程中线段
点,在此过程中线段![]() 的长度
的长度![]() 随着运动时间
随着运动时间![]() 变化的函数关系如图2所示,则边
变化的函数关系如图2所示,则边![]() 的长为__________.
的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,正方形
,正方形![]() 的边长为2,将正方形
的边长为2,将正方形![]() 绕点
绕点![]() 旋转一周,连接
旋转一周,连接![]() 、
、![]() 、
、![]() .
.
(1)猜想:![]() 的值是__________,直线
的值是__________,直线![]() 与直线
与直线![]() 相交所成的锐角度数是__________;
相交所成的锐角度数是__________;
(2)探究:直线![]() 与
与![]() 垂直时,求线段
垂直时,求线段![]() 的长;
的长;
(3)拓展:取![]() 的中点
的中点![]() ,连接
,连接![]() ,直接写出线段
,直接写出线段![]() 长的取值范围.
长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某建筑物![]() 上挂着“巴山渝水,魅力重庆”的宣传条幅
上挂着“巴山渝水,魅力重庆”的宣传条幅![]() ,王同学利用测倾器在斜坡的底部
,王同学利用测倾器在斜坡的底部![]() 处测得条幅底部
处测得条幅底部![]() 的仰角为60°,沿斜坡AB走到B处测得条幅顶部C的仰角为50°.已知斜坡
的仰角为60°,沿斜坡AB走到B处测得条幅顶部C的仰角为50°.已知斜坡![]() 的坡度
的坡度![]() 米,
米,![]() 米(点
米(点![]() 在同平面内,
在同平面内,![]() ,测倾器的高度忽略不计),则条幅
,测倾器的高度忽略不计),则条幅![]() 的长度约为(参考数据:
的长度约为(参考数据:![]()
![]() )
)
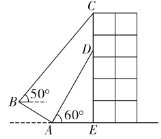
A.12.5米B.12.8米C.13.1米D.13.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:将一个大于0的自然数,去掉其个位数字,再把剩下的数加上原数个位数字的4倍,如果得到的和能被13整除,则称这个数是“一刀两断”数,如果和太大无法直接观察出来,就再次重复这个过程继续计算,例如![]() ,所以55263是“一刀两断”数.
,所以55263是“一刀两断”数.![]() ,所以3247不是“一刀两断”数.
,所以3247不是“一刀两断”数.
(1)判断5928是否为“一刀两断”数:_____(填是或否),并证明任意一个能被13整除的数是“一刀两断”数;
(2)对于一个“一刀两断”数![]() 均为正整数),规定
均为正整数),规定![]()
![]() .若
.若![]() 的千位数字满是
的千位数字满是![]() ,千位数字与十位数字相同,且能被65整除,求出所有满足条件的四位数
,千位数字与十位数字相同,且能被65整除,求出所有满足条件的四位数![]() 中,
中,![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
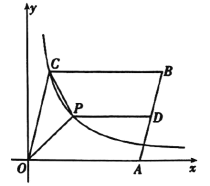
【题目】如图,![]() 的边
的边![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() ,反比例函数
,反比例函数![]() (
(![]() )的图象经过点
)的图象经过点![]() .
.
(1)求反比例函数的关系式和点![]() 的坐标,
的坐标,
(2)过![]() 的中点
的中点![]() 作
作![]() 轴交反比例函数图象于点
轴交反比例函数图象于点![]() ,连接
,连接![]() .求△
.求△![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0;②a-b+c<0;③2a=b;④4a+2b+c>0;⑤若点(-2,y1)和(-![]() ,y2)在该图象上,则y1>y2. 其中正确的结论个数是 ( )
,y2)在该图象上,则y1>y2. 其中正确的结论个数是 ( )
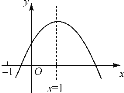
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com