
【题目】定义:将一个大于0的自然数,去掉其个位数字,再把剩下的数加上原数个位数字的4倍,如果得到的和能被13整除,则称这个数是“一刀两断”数,如果和太大无法直接观察出来,就再次重复这个过程继续计算,例如![]() ,所以55263是“一刀两断”数.
,所以55263是“一刀两断”数.![]() ,所以3247不是“一刀两断”数.
,所以3247不是“一刀两断”数.
(1)判断5928是否为“一刀两断”数:_____(填是或否),并证明任意一个能被13整除的数是“一刀两断”数;
(2)对于一个“一刀两断”数![]() 均为正整数),规定
均为正整数),规定![]()
![]() .若
.若![]() 的千位数字满是
的千位数字满是![]() ,千位数字与十位数字相同,且能被65整除,求出所有满足条件的四位数
,千位数字与十位数字相同,且能被65整除,求出所有满足条件的四位数![]() 中,
中,![]() 的最大值.
的最大值.
【答案】(1)是;证明见解析;(2)![]() 的最大值为45.
的最大值为45.
【解析】
(1)根据“一刀两断”数的定义,计算即可得,设任意一个能被13整除的![]() 位数前
位数前![]() 位数字为
位数字为![]() ,个位数字为
,个位数字为![]() ,则这个
,则这个![]() 位数可表示为
位数可表示为![]() ,根据定义进行推理即可证得;
,根据定义进行推理即可证得;
(2)由m能被65整除,得出m是13的倍数也是5的倍数,可得d=0或5,分情况讨论,分别求出满足条件的所有的m的值,代入![]() 中计算即可判断出.
中计算即可判断出.
(1)![]() ,所以5928是“一刀两断”数
,所以5928是“一刀两断”数
证明:设任意一个能被13整除的![]() 位数前
位数前![]() 位数字为
位数字为![]() ,个位数字为
,个位数字为![]() ,则这个
,则这个![]() 位数可表示为
位数可表示为![]() (
(![]() 为正整数),
为正整数),
![]() ,
,
![]() ,
,
![]() 是“一刀两断”数;
是“一刀两断”数;
∴任意一个能被13整除的数是“一刀两断”数,
故答案为:是;
(2)![]() 能被65整除,且a=c,
能被65整除,且a=c,
![]() 既能被13整除又能被5整除.
既能被13整除又能被5整除.
![]() 或
或![]() .
.
当![]() 时,
时,![]() ,
,
![]() 是13的倍数.
是13的倍数.
![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
![]() .
.
当![]() 时,
时,![]() ,
,
![]() 是13的倍数,
是13的倍数,
![]() ,
,
![]() .
.
![]() ,
,
![]() 或
或![]() 或
或![]() .
.
![]() 或
或![]() 或
或![]() .
.
![]() .
.
![]() 的最大值为45,
的最大值为45,
故答案为:45.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形AEHC是由三个全等矩形拼成的,AH与BE、BF、DF、DG、CG分别交于点P、Q、K、M、N,设△BPQ、△DKM、△CNH的面积依次为![]() 、
、![]() 、
、![]() .
.
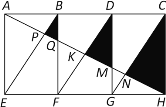
(1)求证:△BPQ∽△DKM∽△CNH;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
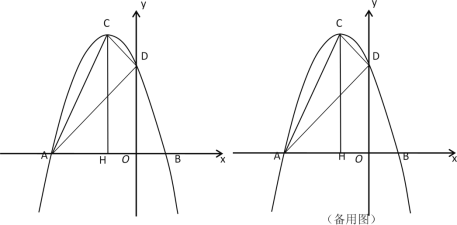
【题目】在平面直角坐标系中,抛物线![]() 与
与![]() 轴的两个交点分别为A(-3,0)、B(1,0),与y轴交于点D(0,3),过顶点C作CH⊥x轴于点H.
轴的两个交点分别为A(-3,0)、B(1,0),与y轴交于点D(0,3),过顶点C作CH⊥x轴于点H.
(1)求抛物线的解析式和顶点C的坐标;
(2)连结AD、CD,若点E为抛物线上一动点(点E与顶点C不重合),当△ADE与△ACD面积相等时,求点E的坐标;
(3)若点P为抛物线上一动点(点P与顶点C不重合),过点P向CD所在的直线作垂线,垂足为点Q,以P、C、Q为顶点的三角形与△ACH相似时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠EOF=60°,在射线OE上取一点A,使OA=10cm,在射线OF上取一点B,使OB=16cm.以OA、OB为邻边作平行四边形OACB.若点P在射线OF上,点Q在线段CA上,且CQ:OP=1:2.设CQ=a(a>0).

(1)连接PQ,当a=2时,求线段PQ的长度.
(2)若以点P、B、C、Q四点为顶点的四边形是平行四边形时,求a的值.
(3)连接PQ,以PQ所在的直线为对称轴,作点C关于直线PQ的对称点C',当点C′恰好落在平行四边形OACB的边上或者边所在的直线上时,直接写出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有5张除正面数字外完全相同的卡片,正面数字分别为1,2,3,4,5,将卡片背面朝上洗匀,从中随机抽出一张记下数字后放回,洗匀后再次随机抽出一张,则抽出的两张卡片上所写数字相同的概率______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A在x轴正半轴上,点B在y轴正半轴上,O为坐标原点,OA=OB=1,过点O作OM1⊥AB于点M1;过点M1作M1A1⊥OA于点A1:过点A1作A1M2⊥AB于点M2;过点M2作M2A2⊥OA于点A2…以此类推,点M2019的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】位于湖北省荆州市滨江公园旁的万寿宝塔始建于明熹靖年间,周边风景秀丽.随着年代的增加,目前塔底低于地面约7米.某校学生先在地面![]() 处侧得塔顶的仰角为30°,再向古塔方向行进
处侧得塔顶的仰角为30°,再向古塔方向行进![]() 米后到达
米后到达![]() 处,在
处,在![]() 处侧得塔顶的仰角为45°(如图所示),已知古塔的整体高度约为40米,那么
处侧得塔顶的仰角为45°(如图所示),已知古塔的整体高度约为40米,那么![]() 的值为_________米.(结果保留根式)
的值为_________米.(结果保留根式)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知D、E、F分别是等边△ABC的边AB、BC、AC上的点,且DE⊥BC、EF⊥AC、FD⊥AB,则下列结论不成立的是( )
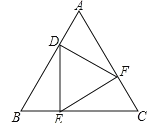
A.△DEF是等边三角形
B.△ADF≌△BED≌△CFE
C.DE=![]() AB
AB
D.S△ABC=3S△DEF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com