
【题目】如图,矩形AEHC是由三个全等矩形拼成的,AH与BE、BF、DF、DG、CG分别交于点P、Q、K、M、N,设△BPQ、△DKM、△CNH的面积依次为![]() 、
、![]() 、
、![]() .
.
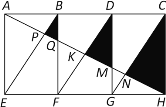
(1)求证:△BPQ∽△DKM∽△CNH;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)详见解析;(2)16
【解析】
(1)利用矩形的性质,平行四边形的判定与性质,和相似三角形的判定定理进行推理即可;
(2)由条件可以得出△ABP∽△ADK∽△ACN,可以求出△ABP与△ADK的相似比为![]() ,△ADK与△ACN相似比为
,△ADK与△ACN相似比为![]() ,由相似三角形的性质,就可以求出K,从而可以求出S2.
,由相似三角形的性质,就可以求出K,从而可以求出S2.
(1)证明:∵矩形AEFB、BFGD、DGHC互相全等,
∴BD=DC=EF=FG,且BD∥EF,DC∥FG,
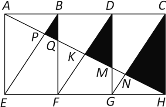
∴四边形BEFD,DFGC为平行四边形,
∴BE∥DF∥CG,
∴∠BPQ=∠DKM=∠CNH,
∵BF∥DG∥CH,
∴∠BQP=∠DMK=∠CHN,
∴△BQP∽△DMK∽△CHN.
(2)∵BP∥DK∥CN,
∴△ABP∽△ADK∽△ACN,
∴![]() ,
,![]() ,
,
由(1)知:△BQP∽△DMK∽△CHN,
∴![]() ,
,![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:
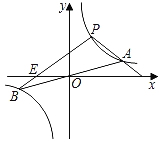
【题目】如图,双曲线y=![]() 与直线y=
与直线y=![]() x交于A、B两点,点P(a,b)在双曲线y=
x交于A、B两点,点P(a,b)在双曲线y=![]() 上,且0<a<4.
上,且0<a<4.
(1)设PB交x轴于点E,若a=1,求点E的坐标;
(2)连接PA、PB,得到△ABP,若4a=b,求△ABP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种高档蔬菜“莼菜”,其进价为16元/kg.经市场调查发现:该商品的日销售量y(kg)是售价x(元/kg)的一次函数,其售价、日销售量对应值如表:
售价 | 20 | 30 | 40 |
日销售量 | 80 | 60 | 40 |
(1)求![]() 关于
关于![]() 的函数解析式(不要求写出自变量的取值范围);
的函数解析式(不要求写出自变量的取值范围);
(2)![]() 为多少时,当天的销售利润
为多少时,当天的销售利润![]() (元)最大?最大利润为多少?
(元)最大?最大利润为多少?
(3)由于产量日渐减少,该商品进价提高了![]() 元/
元/![]() ,物价部门规定该商品售价不得超过36元/
,物价部门规定该商品售价不得超过36元/![]() ,该商店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是864元,求
,该商店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是864元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H交BE于G.下列结论:①BD=CD;②AD+CF=BD;③CE=![]() BF;④AE=BG.其中正确的个数是( )
BF;④AE=BG.其中正确的个数是( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
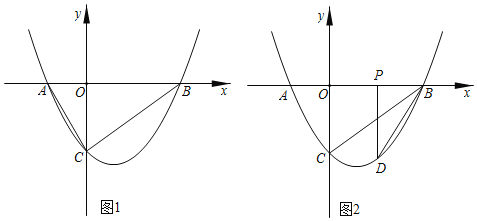
如图1,抛物线y=ax2+bx﹣3与x轴交于A(﹣2,0),B(4,0)两点,与y轴交于点C.
(1)求抛物线的表达式;
(2)点N是抛物线上异于点C的动点,若△NAB的面积与△CAB的面积相等,求出点N的坐标;
(3)如图2,当P为OB的中点时,过点P作PD⊥x轴,交抛物线于点D.连接BD,将△PBD沿x轴向左平移m个单位长度(0<m≤2),将平移过程中△PBD与△OBC重叠部分的面积记为S,求S与m的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:
如图(a),点A、B在直线l的同侧,要在直线l上找一点C,使AC与BC的距离之和最小,我们可以作出点B关于l的对称点B′,连接A B′与直线l交于点C,则点C即为所求.
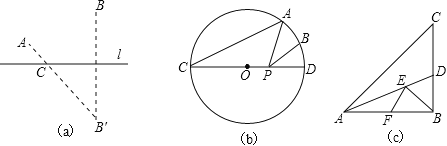
(1)实践运用:
如图(b),已知,⊙O的直径CD为4,点A 在⊙O 上,∠ACD=30°,B 为弧AD 的中点,P为直径CD上一动点,则BP+AP的最小值为 .
(2)知识拓展:
如图(c),在Rt△ABC中,AB=10,∠BAC=45°,∠BAC的平分线交BC于点D,E、F分别是线段AD和AB上的动点,求BE+EF的最小值,并写出解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)8a+7b+2c>0;(3)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;(4)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有().
,y3)在该函数图象上,则y1<y3<y2;(4)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有().
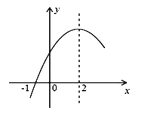
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:将一个大于0的自然数,去掉其个位数字,再把剩下的数加上原数个位数字的4倍,如果得到的和能被13整除,则称这个数是“一刀两断”数,如果和太大无法直接观察出来,就再次重复这个过程继续计算,例如![]() ,所以55263是“一刀两断”数.
,所以55263是“一刀两断”数.![]() ,所以3247不是“一刀两断”数.
,所以3247不是“一刀两断”数.
(1)判断5928是否为“一刀两断”数:_____(填是或否),并证明任意一个能被13整除的数是“一刀两断”数;
(2)对于一个“一刀两断”数![]() 均为正整数),规定
均为正整数),规定![]()
![]() .若
.若![]() 的千位数字满是
的千位数字满是![]() ,千位数字与十位数字相同,且能被65整除,求出所有满足条件的四位数
,千位数字与十位数字相同,且能被65整除,求出所有满足条件的四位数![]() 中,
中,![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com