
����Ŀ���ۺ���̽��
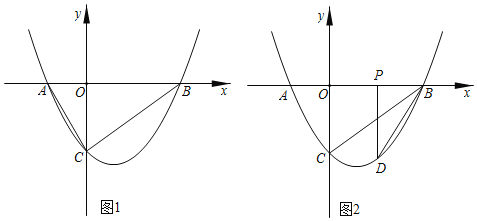
��ͼ1��������y��ax2+bx��3��x�ύ��A����2��0����B��4��0�����㣬��y�ύ�ڵ�C��
��1���������ߵı���ʽ��
��2����N�������������ڵ�C�Ķ��㣬����NAB��������CAB�������ȣ������N�����ꣻ
��3����ͼ2����PΪOB���е�ʱ������P��PD��x�ᣬ���������ڵ�D������BD������PBD��x������ƽ��m����λ���ȣ�0��m��2������ƽ�ƹ����С�PBD���OBC�ص����ֵ������ΪS����S��m�ĺ�����ϵʽ��
���𰸡���1��y��![]() x2��
x2��![]() x��3����2����N�������ǣ�
x��3����2����N�������ǣ�![]() +1��3����
+1��3����![]() +1��3����2����3������3��S����
+1��3����2����3������3��S����![]() m2+
m2+![]() m+
m+![]() ��
��
��������
��1���ѵ�A��B������ֱ���������߽���ʽ���г�����ϵ��a��b�Ľ���ʽ��ͨ���ⷽ����������ǵ�ֵ��
��2���������߽���ʽ��õ�C�����꣬��OC��3�������������ε������ʽ�õ���N��x��ľ���Ϊ3���ݴ��г����̲����
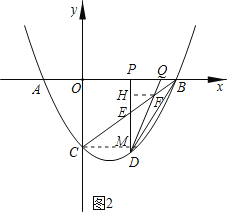
��3����ͼ2������֪�ã�QB��m��PQ��2�����ô���ϵ����ȷ��ֱ��BC�ı���ʽΪy��![]() x��3�����ݶ��κ���ͼ���ϵ������������������ͼ�ε��������D��2����3��������ֱ��CD��x�ᣮ�ɴ����EM�ij��ȣ�����F��FH��PM�ڵ�M���������������Σ���MHF�ס�MPQ�͡�CMF�ס�BQF���������������εĶ�Ӧ�߳ɱ�����֪
x��3�����ݶ��κ���ͼ���ϵ������������������ͼ�ε��������D��2����3��������ֱ��CD��x�ᣮ�ɴ����EM�ij��ȣ�����F��FH��PM�ڵ�M���������������Σ���MHF�ס�MPQ�͡�CMF�ס�BQF���������������εĶ�Ӧ�߳ɱ�����֪![]() ��
��![]() ����MF��k��2��m����QF��km���������ε������ʽ��ͼ�εõ���S��S��PQM��S��EMF��3��
����MF��k��2��m����QF��km���������ε������ʽ��ͼ�εõ���S��S��PQM��S��EMF��3��![]() ����
����![]() m+
m+![]() ����2��m������
����2��m������![]() m2+
m2+![]() m+
m+![]() ��
��
�⣺��1����ͼ1���ѵ�A����2��0����B��4��0���ֱ����y��ax2+bx��3��a��0������
![]() ��
��
���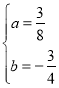 ��
��
���Ը������ߵĽ���ʽΪ��y��![]() x2��
x2��![]() x��3��
x��3��

��2����x��0����y��![]() x2��
x2��![]() x��3����y����3��
x��3����y����3��
���C��������0����3����
��OC��3��
��N��x��y����
��S��NAB��S��CAB��
��|y|��OC��3��
��y����3��
��y��3ʱ��![]() x2��
x2��![]() x��3��3��
x��3��3��
���x��![]() +1��
+1��
��y����3ʱ��![]() x2��
x2��![]() x��3����3��
x��3����3��
���x1��2��x2��0����ȥ����
������������N�������ǣ�![]() +1��3����
+1��3����![]() +1��3����2����3����
+1��3����2����3����
��3����ͼ2������֪�ã�QB��m��PQ��2��
��ֱ��BC�ı���ʽΪy��kx+b��k��0����
��ֱ��y��kx+b������B��4��0����C��0����3����
��![]() ��
��
���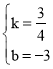 ��
��
��ֱ��BC�ı���ʽΪy��![]() x��3��
x��3��
��0��m��2ʱ������֪��PB��2+m��
��OP��2��m��
��E��2��m����![]() m��
m��![]() ����
����
��OB��4��OP��2��
��x��2����y��![]() x2��
x2��![]() x��3����y����3��
x��3����y����3��
��D��2����3����
��ֱ��CD��x�ᣮ
��EP��![]() m+
m+![]() ��MP��3��
��MP��3��
��EM��MP��EP��3��![]() m��
m��![]() ����
����![]() m+
m+![]() ��
��
����F��FH��PM�ڵ�M�����MHF����MPQ��90�㣮
�ߡ�HMF����PMQ��
���MHF�ס�MPQ��
��![]() ��
��![]() ��
��
�ߡ�FCM����FBQ����FMC����FQB��
���CMF�ס�BQF��
��![]() ��
��![]() ��
��
��CD��2��
��CM��2��m��
��![]() ��
��![]() ��
��
��MF��k��2��m����QF��km��
��MQ��2k��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��PQ��2��
��HF��2��m��
��S��EMF��![]() EMHF��
EMHF��![]() ����
����![]() m+
m+![]() ����2��m����
����2��m����
��S��PQM��![]() PQPM��
PQPM��![]() ��3��2��3��
��3��2��3��
��S��S��PQM��S��EMF��3��![]() ����
����![]() m+
m+![]() ����2��m������
����2��m������![]() m2+
m2+![]() m+
m+![]() ��
��


 ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���BCA��90�㣬DΪAC����һ���㣬OΪBD�е㣬DE��AB������ΪE������OE��CO���ӳ�CO��AB��F�����BAC������������
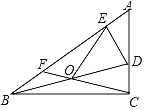
A.��EOF��![]() ��B.��EOF��2��
��B.��EOF��2��
C.��EOF��180�㩁��D.��EOF��180�㩁2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y1��2kx+k�뺯��![]() �������º���y��y2��y1
�������º���y��y2��y1
��1����k��2�����º���y���� ����
��2�����º���y�Ľ���ʽΪy��x2+bx��2����k���� ����b���� ����
��3�����º���y����Ϊ��m��n����
�ٵ�kΪ��ֵʱ��n�д�ֵ����������ֵ��
����n��m�ĺ�������ʽ��
��4������̽��������y1���º���y�ֱ�����B��A������![]() �Ķ���ΪC���º���y�ϴ���һ��D��ʹ���Ե�A��B��C��DΪ������ı���Ϊƽ���ı���ʱ��ֱ��д��k��ֵ��
�Ķ���ΪC���º���y�ϴ���һ��D��ʹ���Ե�A��B��C��DΪ������ı���Ϊƽ���ı���ʱ��ֱ��д��k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AB��DC��AB=AD���Խ���AC��BD���ڵ�O��ACƽ�֡�BAD������C��CE��AB��AB���ӳ����ڵ�E������OE��
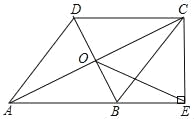
��1����֤���ı���ABCD�����Σ�
��2����AB=![]() ��OE=2�����߶�CE�ij���
��OE=2�����߶�CE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��CE��ABCD�ı�AB�Ĵ�ֱƽ���ߣ�����Ϊ��O��CE��DA���ӳ��߽��ڵ�E������AC��BE��DO��DO��AC���ڵ�F�������н��ۣ����ı���ACBE�����Σ�����ACD����BAE����AF��BE��2��3����S�ı���AFOE��S��COD��2��3�������ĸ�������������ȷ�Ľ����ǣ�������
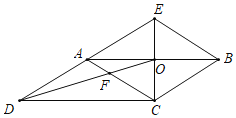
A.�٢�B.�٢ڢ�C.�ڢ�D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������AEHC��������ȫ�Ⱦ���ƴ�ɵģ�AH��BE��BF��DF��DG��CG�ֱ��ڵ�P��Q��K��M��N�����BPQ����DKM����CNH���������Ϊ![]() ��
��![]() ��
��![]() ��
��
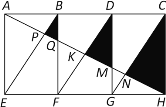
��1����֤����BPQ�ס�DKM�ס�CNH��
��2����![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
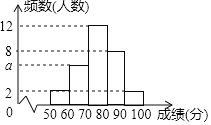
����Ŀ��Ϊ�˽�ij�Ρ�Сѧ���鷨�������ijɼ�����������ȡ��30��ѧ���ijɼ�����ͳ�ƣ�����ͳ����������ͼ��ʾ��Ƶ���ֲ�ֱ��ͼ����֪�ɼ�x����λ���֣������㡰50��x��100��������ͼ����Ϣ�ش��������⣺
��1��ͼ��a��ֵΪ�� ����
��2����Ҫ���Ƹ�����������ͳ��ͼ����ɼ�x�ڡ�70��x��80������Ӧ���ε�Բ�ĽǶ���Ϊ�� ���ȣ�
��3���˴α�������300��ѧ���μӣ�������x��80���ijɼ���Ϊ�����㡱�����á����㡰��ѧ����Լ���� ���ˣ�
��4������Щ���������У�С���ijɼ�Ϊ92�֣����ӳɼ��ڡ�50��x��60���͡�90��x��100����ѧ������ѡ2�ˣ������б�����״ͼ�ķ�������С����ѡ�еĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ƹ�������������μ䡱�������ij��ѧ������ѧ���п���A��ʵ����B��������Զ��C��������D���ܲ����ֻ��Ŀ��Ϊ���˽�ѧ����������Ŀ��ϲ������������ȡ�˲���ѧ�����е��飬�������������Ƴ���ͼ�٢���ͳ��ͼ������ͼ�е���Ϣ����������⣺
��1������������У��������˶�����ѧ����
��2������㱾�������ϲ����������Զ����ѧ����������ռ�ٷֱȣ���������ͳ��ͼ����������
��3�������鵽ϲ������������5��ѧ������3��������2��Ů�����ִ���5��ѧ���������ȡ2��ѧ�������û���״ͼ���б��ķ���������պó鵽ͬ�Ա�ѧ���ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������5�ų�������������ȫ��ͬ�Ŀ�Ƭ���������ֱַ�Ϊ1��2��3��4��5������Ƭ���泯��ϴ�ȣ�����������һ�ż������ֺ�Żأ�ϴ�Ⱥ��ٴ�������һ�ţ����������ſ�Ƭ����д������ͬ�ĸ���______��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com