
【题目】如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H交BE于G.下列结论:①BD=CD;②AD+CF=BD;③CE=![]() BF;④AE=BG.其中正确的个数是( )
BF;④AE=BG.其中正确的个数是( )

A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
根据∠ABC=45°,CD⊥AB可得出BD=CD,利用AAS判定Rt△DFB≌Rt△DAC,从而得出DF=AD,BF=AC.则CD=CF+AD,即AD+CF=BD;再利用AAS判定Rt△BEA≌Rt△BEC,得出CE=AE=![]() AC,又因为BF=AC所以CE=
AC,又因为BF=AC所以CE=![]() AC=
AC=![]() BF,连接CG.因为△BCD是等腰直角三角形,即BD=CD.又因为DH⊥BC,那么DH垂直平分BC.即BG=CG.在Rt△CEG中,CG是斜边,CE是直角边,所以CE<CG.即AE<BG.
BF,连接CG.因为△BCD是等腰直角三角形,即BD=CD.又因为DH⊥BC,那么DH垂直平分BC.即BG=CG.在Rt△CEG中,CG是斜边,CE是直角边,所以CE<CG.即AE<BG.
解:∵CD⊥AB,∠ABC=45°,
∴△BCD是等腰直角三角形.
∴BD=CD.故①正确;
在Rt△DFB和Rt△DAC中,
∵∠DBF=90°﹣∠BFD,∠DCA=90°﹣∠EFC,且∠BFD=∠EFC,
∴∠DBF=∠DCA.
又∵∠BDF=∠CDA=90°,BD=CD,
∴△DFB≌△DAC.
∴BF=AC;DF=AD.
∵CD=CF+DF,
∴AD+CF=BD;故②正确;
在Rt△BEA和Rt△BEC中
∵BE平分∠ABC,
∴∠ABE=∠CBE.
又∵BE=BE,∠BEA=∠BEC=90°,
∴Rt△BEA≌Rt△BEC.
∴CE=AE=![]() AC.
AC.
又由(1),知BF=AC,
∴CE=![]() AC=
AC=![]() BF;故③正确;
BF;故③正确;
连接CG.
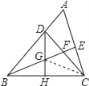
∵△BCD是等腰直角三角形,
∴BD=CD
又DH⊥BC,
∴DH垂直平分BC.
∴BG=CG
在Rt△CEG中,
∵CG是斜边,CE是直角边,
∴CE<CG.
∵CE=AE,
∴AE<BG.故④错误.
故选:C.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】为提高节水意识,小明随机统计了自己家7天的用水量,并分析了第3天的用水情况,将得到的数据进行整理后,绘制成如图所示的统计图.(单位:升)
每天用水折线统计图 第3天用水情况条形统计图
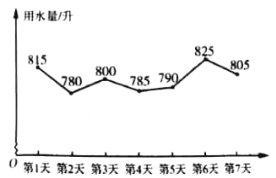
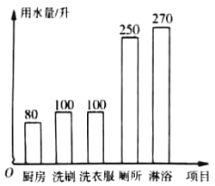
(1)填空:这7天内小明家里每天用水量的平均数为 升、中位数为 升;
(2)求第3天小明家淋浴的水占这一天总用水量的百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
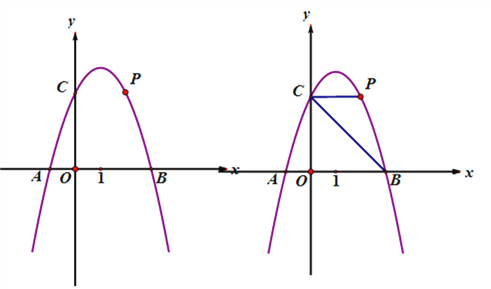
【题目】如图,抛物线![]() 交X轴于点A、B(A左B右),交Y轴于点C,
交X轴于点A、B(A左B右),交Y轴于点C, ![]()
=6,点P为第一象限内抛物线上的一点.
(1)求抛物线的解析式;
(2)若∠PCB=45°,求点P的坐标;
(3)点Q为第四象限内抛物线上一点,点Q的横坐标比点P的横坐标大1,连接PC、
AQ,当PC=![]() AQ时,求点P的坐标以及ΔPCQ的面积.
AQ时,求点P的坐标以及ΔPCQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(-2,0),C(2,2),过C作CB⊥x轴于B.
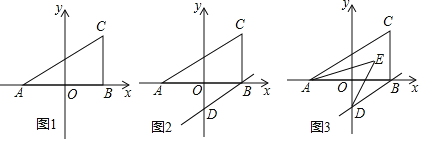
(1)如图1,△ABC的面积是 ;
(2)如图1,在y轴上找一点P,使得△ABP的面积与△ABC的面积相等,请直接写出P点坐标: ;
(3)如图2,若过B作BD∥AC交y轴于D,则∠BAC+∠ODB的度数为 度;
(4)如图3,BD∥AC,若AE、DE分别平分∠CAB,∠ODB,求∠AED的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】6张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
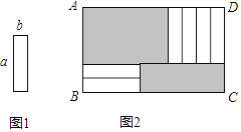
A. a=2b B. a=3b C. a=4b D. a=b
查看答案和解析>>
科目:初中数学 来源: 题型:
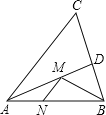
【题目】如图,在锐角△ABC中,AB=4![]() ,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是______.
,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图(2)所示,当P运动到BC中点时,△PAD的面积为( )
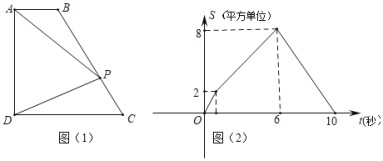
A. 4B. 5C. 6D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图表示购买某种商品的个数与付款数之间的关系
(1)根据图形完成下列表格
购买商品个数(个) | 2 | 4 | 6 | 7 |
付款数(元) |
|
|
|
|
(2)请写出表示付款数y(元)与购买这种商品的个数x(个)之间的关系式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com