
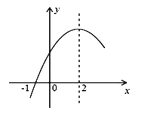
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)8a+7b+2c>0;(3)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;(4)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有().
,y3)在该函数图象上,则y1<y3<y2;(4)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有().
A.1个B.2个C.3个D.4个
【答案】C
【解析】
根据抛物线的对称轴为直线x=2,可判断(1),利用x=-1时,y=0,则a-b+c=0,结合对称轴可得c=-5a,所以8a+7b+2c=8a-28a-10a=-30a,再根据抛物线开口向下可判断(2),利用抛物线的对称性得到C关于对称轴对称的点的坐标![]() ,然后利用二次函数的增减性即可得到判断(3),作出直线y=-3,然后依据函数图象进行判断,即可判断(4).
,然后利用二次函数的增减性即可得到判断(3),作出直线y=-3,然后依据函数图象进行判断,即可判断(4).
解:∵![]() ,
,
∴4a+b=0,故(1)正确.
∵抛物线与x轴的一个交点为(-1,0),
∴a-b+c=0
又∵b=-4a,
∴a+4a+c=0,即c=-5a,
∴8a+7b+2c=8a-28a-10a=-30a,
∵抛物线开口向下,
∴a<0,
∴8a+7b+2c>0,故(2)正确;
∵抛物线的对称轴为x=2,C(![]() ,
,![]() ),
),
∴C关于对称轴对称的点坐标(![]() ,
,![]() ).
).
∵-3<![]() <
<![]() ,在对称轴的左侧,
,在对称轴的左侧,
∴y随x的增大而增大,
∴![]() ,故(3)错误.
,故(3)错误.
方程a(x+1)(x-5)=0的两根为x=-1或x=5,
过y=-3作x轴的平行线,直线y=-3与抛物线的交点的横坐标为方程的两根,
依据函数图象可知:![]() . 故(4)正确.
. 故(4)正确.
故选C..
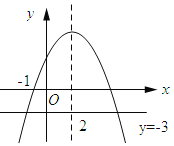


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ;抛物线
;抛物线![]()
![]() 过
过![]() ,
,![]() 两点,与
两点,与![]() 轴交于另一点
轴交于另一点![]() ,抛物线的顶点为
,抛物线的顶点为![]() .
.
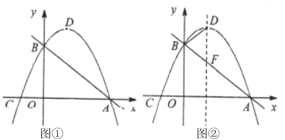
(1)求抛物线的解析式;
(2)在直线![]() 上方的抛物线上有一动点
上方的抛物线上有一动点![]() ,求出点
,求出点![]() 到直线
到直线![]() 的距离的最大值;
的距离的最大值;
(3)如图②,直线![]() 与抛物线的对称轴相交于点
与抛物线的对称轴相交于点![]() ,请直接写出
,请直接写出![]() 的平分线与
的平分线与![]() 轴的交点
轴的交点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形AEHC是由三个全等矩形拼成的,AH与BE、BF、DF、DG、CG分别交于点P、Q、K、M、N,设△BPQ、△DKM、△CNH的面积依次为![]() 、
、![]() 、
、![]() .
.
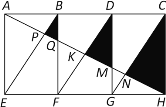
(1)求证:△BPQ∽△DKM∽△CNH;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七、八、九年级共有1000名学生.学校统计了各年级学生的人数,绘制了图①、图②两幅不完整的统计图.
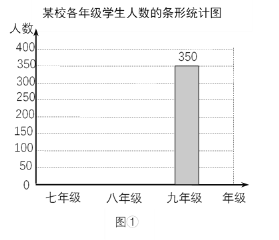
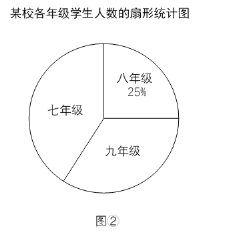
(1)将图①的条形统计图补充完整.
(2)图②中,表示七年级学生人数的扇形的圆心角度数为 °.
(3)学校数学兴趣小组调查了各年级男生的人数,绘制了如图③所示的各年级男生人数占比的折线统计图(年级男生人数占比=该年级男生人数÷该年级总人数×100%).请结合相关信息,绘制一幅适当的统计图,表示各年级男生及女生的人数,并在图中标明相应的数据.
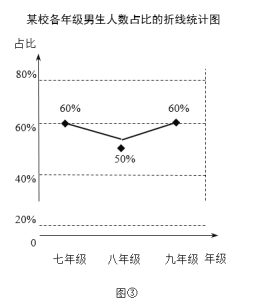
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推广阳光体育“大课间”活动,我市某中学决定在学生中开设A:实心球.B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;
(3)若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在云南大理坐落着美丽的大理三塔.数学活动小组开展课外实践活动,在一个阳光明媚的上午,他们去测量三塔中一塔的高度,携带的测量工具有:测角仪.皮尺.小镜子.
(1)小华利用测角仪和皮尺测量塔高. 图1为小华测量塔高的示意图.她先在塔前的平地上选择一点![]() ,用测角仪测出看塔顶
,用测角仪测出看塔顶![]() 的仰角
的仰角![]() ,在
,在![]() 点和塔之间选择一点
点和塔之间选择一点![]() ,测出看塔顶
,测出看塔顶![]() 的仰角
的仰角![]() ,然后用皮尺量出
,然后用皮尺量出![]() .
.![]() 两点的距离为
两点的距离为![]() m,自身的高度为
m,自身的高度为![]() m.请你利用上述数据帮助小华计算出塔的高度(
m.请你利用上述数据帮助小华计算出塔的高度(![]() ,结果保留整数).
,结果保留整数).
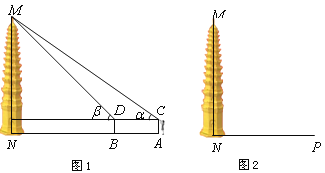
(2)如果你是活动小组的一员,正准备测量塔高,而此时塔影![]() 的长为
的长为![]() m(如图2),你能否利用这一数据设计一个测量方案?如果能,
m(如图2),你能否利用这一数据设计一个测量方案?如果能,
请回答下列问题:
①在你设计的测量方案中,选用的测量工具是: ;
②要计算出塔的高,你还需要测量哪些数据? .
查看答案和解析>>
科目:初中数学 来源: 题型:
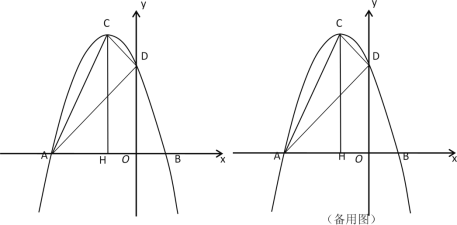
【题目】在平面直角坐标系中,抛物线![]() 与
与![]() 轴的两个交点分别为A(-3,0)、B(1,0),与y轴交于点D(0,3),过顶点C作CH⊥x轴于点H.
轴的两个交点分别为A(-3,0)、B(1,0),与y轴交于点D(0,3),过顶点C作CH⊥x轴于点H.
(1)求抛物线的解析式和顶点C的坐标;
(2)连结AD、CD,若点E为抛物线上一动点(点E与顶点C不重合),当△ADE与△ACD面积相等时,求点E的坐标;
(3)若点P为抛物线上一动点(点P与顶点C不重合),过点P向CD所在的直线作垂线,垂足为点Q,以P、C、Q为顶点的三角形与△ACH相似时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠EOF=60°,在射线OE上取一点A,使OA=10cm,在射线OF上取一点B,使OB=16cm.以OA、OB为邻边作平行四边形OACB.若点P在射线OF上,点Q在线段CA上,且CQ:OP=1:2.设CQ=a(a>0).

(1)连接PQ,当a=2时,求线段PQ的长度.
(2)若以点P、B、C、Q四点为顶点的四边形是平行四边形时,求a的值.
(3)连接PQ,以PQ所在的直线为对称轴,作点C关于直线PQ的对称点C',当点C′恰好落在平行四边形OACB的边上或者边所在的直线上时,直接写出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知D、E、F分别是等边△ABC的边AB、BC、AC上的点,且DE⊥BC、EF⊥AC、FD⊥AB,则下列结论不成立的是( )
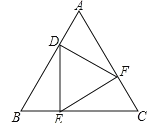
A.△DEF是等边三角形
B.△ADF≌△BED≌△CFE
C.DE=![]() AB
AB
D.S△ABC=3S△DEF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com