
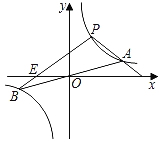
【题目】如图,双曲线y=![]() 与直线y=
与直线y=![]() x交于A、B两点,点P(a,b)在双曲线y=
x交于A、B两点,点P(a,b)在双曲线y=![]() 上,且0<a<4.
上,且0<a<4.
(1)设PB交x轴于点E,若a=1,求点E的坐标;
(2)连接PA、PB,得到△ABP,若4a=b,求△ABP的面积.
【答案】(1)点E的坐标为(﹣3,0);(2)15.
【解析】
(1)解方程组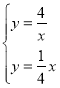 得A(4,1),B(﹣4,﹣1),再利用反比例函数解析式确定P(1,4),则可根据待定系数法求出直线PB的解析式为y=x+3,从而计算出函数值为0对应的函数值得到点E的坐标;
得A(4,1),B(﹣4,﹣1),再利用反比例函数解析式确定P(1,4),则可根据待定系数法求出直线PB的解析式为y=x+3,从而计算出函数值为0对应的函数值得到点E的坐标;
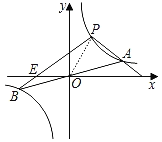
(2)利用反比例函数图象上点的坐标特征得到ab=4,加上b=4a,则可求出a、b得到P(1,4),连接OP,如图,由(1)得此时E点坐标为(﹣3,0),接着利用三角形面积公式计算出S△POB=![]() ,由于点A与点B关于原点对称,所以OA=OB,所以S△BAP=2S△OBP.
,由于点A与点B关于原点对称,所以OA=OB,所以S△BAP=2S△OBP.
解:(1)解方程组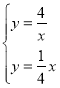
得![]() 或
或![]() ,
,
∴A(4,1),B(﹣4,﹣1),
当x=1时,y=![]() =4,则P(1,4),
=4,则P(1,4),
设直线PB的解析式为y=mx+n,
把P(1,4),B(﹣4,﹣1)代入得![]() ,
,
解得![]() ,
,
∴直线PB的解析式为y=x+3,
当y=0时,x+3=0,解得x=﹣3,
∴点E的坐标为(﹣3,0);
(2)∵点P(a,b)在双曲线y=![]() 上,
上,
∴ab=4,
而b=4a,
∴a4a=4,解得a=±1,
∵0<a<4.
∴a=1,
∴P(1,4),
连接OP,如图,由(1)得此时E点坐标为(﹣3,0),
S△POB=S△OBE+S△OEP=![]() ×3×1+
×3×1+![]() ×3×4=
×3×4=![]() ,
,
∵点A与点B关于原点对称,
∴OA=OB,
∴S△OAP=S△OBP=![]() ,
,
∴S△BAP=2S△OBP=15.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】为了解某校初二学生每周上网的时间,两位学生进行了抽样调查.小丽调查了初二电脑爱好者中40名学生每周上网的时间;小杰从全校400名初二学生中随机抽取了40名学生,调查了每周上网的时间.小丽与小杰整理各自样本数据,如下表所示:
时间段 (小时/周) | 小丽抽样 人数 | 小杰抽样 人数 |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(每组可含最低值,不含最高值)

(1)你认为哪位同学抽取的样本不合理?请说明理由;
(2)根据合理抽取的样本,把上图中的频数分布直方图补画完整;
(3)专家建议每周上网2小时以上(含2小时)的同学应适当减少上网的时间,估计该校全体初二学生中有多少名同学应适当减少上网的时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
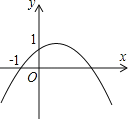
【题目】如图,二次函数![]() (a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②
(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②![]() >4a,③0<b<1,④当x>﹣1时,y>0,其中正确结论的个数是( )
>4a,③0<b<1,④当x>﹣1时,y>0,其中正确结论的个数是( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3的图象经过点(1,﹣4)和(﹣1,0).
(1)求这个二次函数的表达式;
(2)x在什么范围内,y随x增大而减小?该函数有最大值还是有最小值?求出这个最值.
查看答案和解析>>
科目:初中数学 来源: 题型:
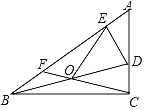
【题目】如图,在△ABC中,∠BCA=90°,D为AC边上一动点,O为BD中点,DE⊥AB,垂足为E,连结OE,CO,延长CO交AB于F,设∠BAC=α,则( )
A.∠EOF=![]() αB.∠EOF=2α
αB.∠EOF=2α
C.∠EOF=180°﹣αD.∠EOF=180°﹣2α
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E是AD边中点,BD、CE交于点H,BE、AH交于点G,则下列结论:
①AG⊥BE;②BG=4GE;③S△BHE=S△CHD;④∠AHB=∠EHD.
其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党中央提出的“惠民政策”,我市今年计划开发建设A、B两种户型的“廉租房”共40套.投入资金不超过200万元,又不低于198万元.开发建设办公室预算:一套A型“廉租房”的造价为5.2万元,一套B型“廉租房”的造价为4.8万元.
(1)请问有几种开发建设方案?
(2)哪种建设方案投入资金最少?最少资金是多少万元?
(3)在(2)的方案下,为了让更多的人享受到“惠民”政策,开发建设办公室决定通过缩小“廉租房”的面积来降低造价、节省资金.每套A户型“廉租房”的造价降低0.7万元,每套B户型“廉租房”的造价降低0.3万元,将节省下来的资金全部用于再次开发建设缩小面积后的“廉租房”,如果同时建设A、B两种户型,请你直接写出再次开发建设的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ;抛物线
;抛物线![]()
![]() 过
过![]() ,
,![]() 两点,与
两点,与![]() 轴交于另一点
轴交于另一点![]() ,抛物线的顶点为
,抛物线的顶点为![]() .
.
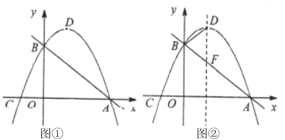
(1)求抛物线的解析式;
(2)在直线![]() 上方的抛物线上有一动点
上方的抛物线上有一动点![]() ,求出点
,求出点![]() 到直线
到直线![]() 的距离的最大值;
的距离的最大值;
(3)如图②,直线![]() 与抛物线的对称轴相交于点
与抛物线的对称轴相交于点![]() ,请直接写出
,请直接写出![]() 的平分线与
的平分线与![]() 轴的交点
轴的交点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形AEHC是由三个全等矩形拼成的,AH与BE、BF、DF、DG、CG分别交于点P、Q、K、M、N,设△BPQ、△DKM、△CNH的面积依次为![]() 、
、![]() 、
、![]() .
.
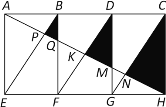
(1)求证:△BPQ∽△DKM∽△CNH;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com