
【题目】为了解某校初二学生每周上网的时间,两位学生进行了抽样调查.小丽调查了初二电脑爱好者中40名学生每周上网的时间;小杰从全校400名初二学生中随机抽取了40名学生,调查了每周上网的时间.小丽与小杰整理各自样本数据,如下表所示:
时间段 (小时/周) | 小丽抽样 人数 | 小杰抽样 人数 |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(每组可含最低值,不含最高值)

(1)你认为哪位同学抽取的样本不合理?请说明理由;
(2)根据合理抽取的样本,把上图中的频数分布直方图补画完整;
(3)专家建议每周上网2小时以上(含2小时)的同学应适当减少上网的时间,估计该校全体初二学生中有多少名同学应适当减少上网的时间?
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的
5个主题进行了抽样调查(每位同学只选取最关注的一个),根据调查结果绘制了两幅不完
整的统计图,根据图中提供的信息,解答下列问题:
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整;
(3)在扇形统计图中“进取”部分扇形的圆心角是 度;
(4)若该校学生人数为800人,请根据上述调查结果,估计该校学生中“感恩”的人数.
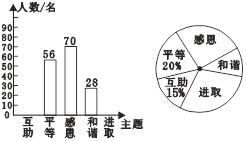
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线l:
中,直线l:![]() 与直线
与直线![]() ,直线
,直线![]() 分别交于点A,B,直线
分别交于点A,B,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(1)求直线![]() 与
与![]() 轴的交点坐标;
轴的交点坐标;
(2)横、纵坐标都是整数的点叫做整点.记线段![]() 围成的区域(不含边界)为
围成的区域(不含边界)为![]() .
.
①当![]() 时,结合函数图象,求区域
时,结合函数图象,求区域![]() 内的整点个数;
内的整点个数;
②若区域![]() 内没有整点,直接写出
内没有整点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,
,![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 为抛物线的顶点,
为抛物线的顶点,![]() 轴于点
轴于点![]() ,且
,且![]() .
.

(1)求抛物线的解析式;
(2)做点![]() 与
与![]() 点关于对称轴对称,连接
点关于对称轴对称,连接![]() ,过点
,过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 是第一象限内抛物线上一点,连接
是第一象限内抛物线上一点,连接![]() 与
与![]() 相交于点
相交于点![]() ,过点
,过点![]() 做
做![]() 轴于点
轴于点![]() ,
,![]() 与
与![]() 相交于
相交于![]() ,连接
,连接![]() ,若
,若![]() ,求
,求![]() 点的坐标和
点的坐标和![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,10×10的网格中,A,B,C均在格点上,诮用无刻度的直尺作直线MN,使得直线MN平分△ABC的周长(留作图痕迹,不写作法)
(1)请在图1中作出符合要求的一条直线MN;
(2)如图2,点M为BC上一点,BM=5.请在AB上作出点N的位置.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,老旧电视机屏幕的长宽比为4︰3,但是多数电影图像的长宽比为2.4︰1,故在播放电影时电视机屏幕的上方和下方会有两条等宽的黑色带子.
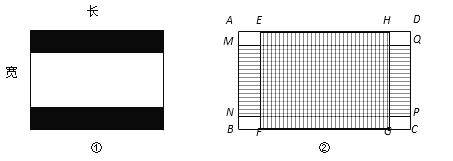
(1)若图①中电视机屏幕为20寸(即屏幕对角线长度):
①该屏幕的长= 寸,宽= 寸;
②已知“屏幕浪费比=黑色带子的总面积:电视机屏幕的总面积”,求该电视机屏幕的浪费比.
(2) 为了兼顾电影的收视需求,一种新的屏幕的长宽比诞生了.如图②,这种屏幕(矩形ABCD)恰好包含面积相等且长宽比分别为4︰3的屏幕(矩形EFGH)与2.4︰1的屏幕(矩形MNPQ).求这种屏幕的长宽比.(参考数据:![]() ≈2.2,结果精确到0.1)
≈2.2,结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
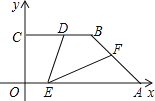
【题目】如图,直角梯形OABC的直角顶点是坐标原点,边OA,OC分别在x轴,y轴的正半轴上.OA∥BC,D是BC上一点,BD=![]() OA=
OA=![]() ,AB=3,∠OAB=45°,E,F分别是线段OA,AB上的两个动点,且始终保持∠DEF=45°.设OE=x,AF=y,则y与x的函数关系式为_____.
,AB=3,∠OAB=45°,E,F分别是线段OA,AB上的两个动点,且始终保持∠DEF=45°.设OE=x,AF=y,则y与x的函数关系式为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
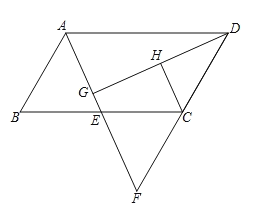
【题目】如图,四边形![]() 为平行四边形,
为平行四边形,![]() 为
为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:△![]() ≌△
≌△![]() ;
;
(2)过点![]() 作
作![]() 于点
于点![]() ,
,![]() 为
为![]() 的中点.判断
的中点.判断![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
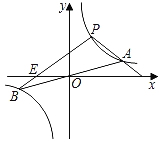
【题目】如图,双曲线y=![]() 与直线y=
与直线y=![]() x交于A、B两点,点P(a,b)在双曲线y=
x交于A、B两点,点P(a,b)在双曲线y=![]() 上,且0<a<4.
上,且0<a<4.
(1)设PB交x轴于点E,若a=1,求点E的坐标;
(2)连接PA、PB,得到△ABP,若4a=b,求△ABP的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com