
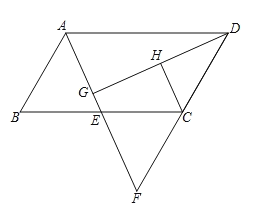
【题目】如图,四边形![]() 为平行四边形,
为平行四边形,![]() 为
为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:△![]() ≌△
≌△![]() ;
;
(2)过点![]() 作
作![]() 于点
于点![]() ,
,![]() 为
为![]() 的中点.判断
的中点.判断![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
【答案】(1)见解析;(2)CH⊥DG,见解析
【解析】
(1)由平行四边形的性质可得:AB‖DC,则可求出∠BAE=∠CFE,结合题目条件可证得结论;
(2)由(1)可证得CF=CD,可得CH为三角形DFG的中位线,则可得CH‖AF,可证CH⊥DG.
(1)证明:∵四边形ABCD为平行四边形,
∴AB‖DC,
∴∠BAE=∠CFE,
∵E为BC的中点,
∴BE=CE,
在△ABE和△FCE中:
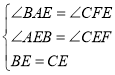 ,
,
∴△ABE![]() △FCE(AAS);
△FCE(AAS);
(2)解:CH⊥DG,
理由如下:由(1)得△ABE![]() △FCE,
△FCE,
∴AB=CF,
∵四边形ABCD为平行四边形,
∴AB=CD,
∴CF=CD,
∴C为FD的中点,
∵![]() 为
为![]() 的中点,
的中点,
∴CH为△DFG的中位线,
∴CH‖AF,
∵DG⊥AE,
∴∠DHC=∠DGF=90°,
∴DG⊥AE.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E为DC的中点,AD:AB=![]() :2,CP:BP=1:2,连接EP并延长,交AB的延长线于点F,AP、BE相交于点O.下列结论:①EP平分∠CEB;②
:2,CP:BP=1:2,连接EP并延长,交AB的延长线于点F,AP、BE相交于点O.下列结论:①EP平分∠CEB;②![]() =PBEF;③PFEF=2
=PBEF;③PFEF=2![]() ;④EFEP=4AOPO.其中正确的是( )
;④EFEP=4AOPO.其中正确的是( )
A. ①②③B. ①②④C. ①③④D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校初二学生每周上网的时间,两位学生进行了抽样调查.小丽调查了初二电脑爱好者中40名学生每周上网的时间;小杰从全校400名初二学生中随机抽取了40名学生,调查了每周上网的时间.小丽与小杰整理各自样本数据,如下表所示:
时间段 (小时/周) | 小丽抽样 人数 | 小杰抽样 人数 |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(每组可含最低值,不含最高值)

(1)你认为哪位同学抽取的样本不合理?请说明理由;
(2)根据合理抽取的样本,把上图中的频数分布直方图补画完整;
(3)专家建议每周上网2小时以上(含2小时)的同学应适当减少上网的时间,估计该校全体初二学生中有多少名同学应适当减少上网的时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是为(0,3)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.

(1)若抛物线过点C、A、A′,求此抛物线的解析式;
(2)求平行四边形ABOC和平行四边形A′B′OC′重叠部分△OC′D的周长;
(3)点M是第一象限内抛物线上的一动点,问:点M在何处时;△AMA′的面积最大?最大面积是多少?并求出此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备购进![]() 两种商品,
两种商品,![]() 种商品毎件的进价比
种商品毎件的进价比![]() 种商品每件的进价多20元,用3000元购进
种商品每件的进价多20元,用3000元购进![]() 种商品和用1800元购进
种商品和用1800元购进![]() 种商品的数量相同.商店将
种商品的数量相同.商店将![]() 种商品每件的售价定为80元,
种商品每件的售价定为80元,![]() 种商品每件的售价定为45元.
种商品每件的售价定为45元.
(1)![]() 种商品每件的进价和
种商品每件的进价和![]() 种商品每件的进价各是多少元?
种商品每件的进价各是多少元?
(2)商店计划用不超过1560元的资金购进![]() 两种商品共40件,其中
两种商品共40件,其中![]() 种商品的数量不低于
种商品的数量不低于![]() 种商品数量的一半,该商店有几种进货方案?
种商品数量的一半,该商店有几种进货方案?
(3)端午节期间,商店开展优惠促销活动,决定对每件![]() 种商品售价优惠
种商品售价优惠![]() (
(![]() )元,
)元,![]() 种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.
种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学团委组织征文活动,并设立若干奖项.学校计划派人根据设奖情况去购买![]() 三种奖品共
三种奖品共![]() 件,其中
件,其中![]() 型奖品件数比
型奖品件数比![]() 型奖品件数的
型奖品件数的![]() 倍少
倍少![]() 件,
件,![]() 型奖品所花费用不超过
型奖品所花费用不超过![]() 型奖品所花费用的
型奖品所花费用的![]() 倍.各种奖品的单价如右表所示.如果计划
倍.各种奖品的单价如右表所示.如果计划![]() 型奖品买
型奖品买![]() 件,买
件,买![]() 件奖品的总费用是
件奖品的总费用是![]() 元.
元.
|
|
| |
单价(元) |
|
|
|
(1)试求![]() 与
与![]() 之间的函数关系式,并求出自变量
之间的函数关系式,并求出自变量![]() 的取值范围;
的取值范围;
(2)请你设计一种方案,使得购买这三种奖品所花的总费用最少,并求出最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() (a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②
(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②![]() >4a,③0<b<1,④当x>﹣1时,y>0,其中正确结论的个数是( )
>4a,③0<b<1,④当x>﹣1时,y>0,其中正确结论的个数是( )
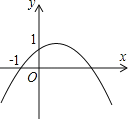
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3的图象经过点(1,﹣4)和(﹣1,0).
(1)求这个二次函数的表达式;
(2)x在什么范围内,y随x增大而减小?该函数有最大值还是有最小值?求出这个最值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ;抛物线
;抛物线![]()
![]() 过
过![]() ,
,![]() 两点,与
两点,与![]() 轴交于另一点
轴交于另一点![]() ,抛物线的顶点为
,抛物线的顶点为![]() .
.
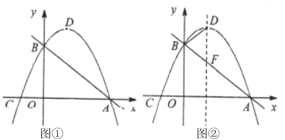
(1)求抛物线的解析式;
(2)在直线![]() 上方的抛物线上有一动点
上方的抛物线上有一动点![]() ,求出点
,求出点![]() 到直线
到直线![]() 的距离的最大值;
的距离的最大值;
(3)如图②,直线![]() 与抛物线的对称轴相交于点
与抛物线的对称轴相交于点![]() ,请直接写出
,请直接写出![]() 的平分线与
的平分线与![]() 轴的交点
轴的交点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com