
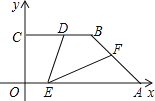
【题目】如图,直角梯形OABC的直角顶点是坐标原点,边OA,OC分别在x轴,y轴的正半轴上.OA∥BC,D是BC上一点,BD=![]() OA=
OA=![]() ,AB=3,∠OAB=45°,E,F分别是线段OA,AB上的两个动点,且始终保持∠DEF=45°.设OE=x,AF=y,则y与x的函数关系式为_____.
,AB=3,∠OAB=45°,E,F分别是线段OA,AB上的两个动点,且始终保持∠DEF=45°.设OE=x,AF=y,则y与x的函数关系式为_____.
【答案】![]()
【解析】
首先过B作x轴的垂线,设垂足为M,由已知易求得OA=4![]() ,在Rt△ABM中,已知∠OAB的度数及AB的长,即可求出AM、BM的长,进而可得到BC、CD的长,再连接OD,证△ODE∽△AEF,通过得到的比例线段,即可得出y与x的函数关系式.
,在Rt△ABM中,已知∠OAB的度数及AB的长,即可求出AM、BM的长,进而可得到BC、CD的长,再连接OD,证△ODE∽△AEF,通过得到的比例线段,即可得出y与x的函数关系式.
解:过B作BM⊥x轴于M.
在Rt△ABM中,
∵AB=3,∠BAM=45°,
∴AM=BM=![]() ,
,
∵BD=![]() OA=
OA=![]() ,
,
![]() ,
,
∴BC=OA﹣AM=4![]() ﹣
﹣![]()
![]() ,CD=BC﹣BD=
,CD=BC﹣BD=![]() ,
,
∴D(![]() ,
,![]() ),
),
![]() .
.
连接OD,则点D在∠COA的平分线上,所以∠DOE=∠COD=45°.
又∵在梯形DOAB中,∠BAO=45°,
∴由三角形外角定理得:∠ODE=∠DEA﹣45°,又∠AEF=∠DEA﹣45°,
∴∠ODE
=∠AEF,
∴△ODE∽△AEF,
![]()
即![]()
∴y与x的解析式为:![]() .
.
故答案为:![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一家商店经营一种玩具,进价为每件50元,调查市场发现日销售量y(件)是关于售价x(元/件)的一次函数,相关数据如表,商店每天的总支出是600元.
售价(元/件) | 50 | 55 | 60 | 65 |
日销售量y/件 | 80 | 70 | 60 | 50 |
(1)直接写出y与x之间的函数关系式.(不要求写出自变量x的取值范围)
(2)商店在“五一”这天尽可能优惠顾客,正好收支平衡(收入=支出),问当天玩具的售价为多少元/件.
(3)商店最早需要多少天,纯利可以突破万元,玩具的售价应定为多少元/件?(每天纯利=每天的销售额﹣成本﹣每天的支出)
查看答案和解析>>
科目:初中数学 来源: 题型:
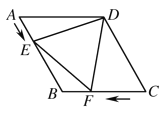
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 同时由
同时由![]() ,
,![]() 两点出发,分别沿
两点出发,分别沿![]() ,
,![]() 方向向点
方向向点![]() 匀速运动,点
匀速运动,点![]() 的运动速度为
的运动速度为![]() ,点
,点![]() 的运动速度为
的运动速度为![]() ,点
,点![]() 到达点
到达点![]() 后,点
后,点![]() 与点
与点![]() 同时停止运动.若运动时间为
同时停止运动.若运动时间为![]() 秒时,
秒时,![]() 为等边三角形,则
为等边三角形,则![]() 的值为__________.
的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校初二学生每周上网的时间,两位学生进行了抽样调查.小丽调查了初二电脑爱好者中40名学生每周上网的时间;小杰从全校400名初二学生中随机抽取了40名学生,调查了每周上网的时间.小丽与小杰整理各自样本数据,如下表所示:
时间段 (小时/周) | 小丽抽样 人数 | 小杰抽样 人数 |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(每组可含最低值,不含最高值)

(1)你认为哪位同学抽取的样本不合理?请说明理由;
(2)根据合理抽取的样本,把上图中的频数分布直方图补画完整;
(3)专家建议每周上网2小时以上(含2小时)的同学应适当减少上网的时间,估计该校全体初二学生中有多少名同学应适当减少上网的时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 过点
过点![]() ,且与直线
,且与直线![]() 交于B、C两点,点B的坐标为
交于B、C两点,点B的坐标为![]() .
.
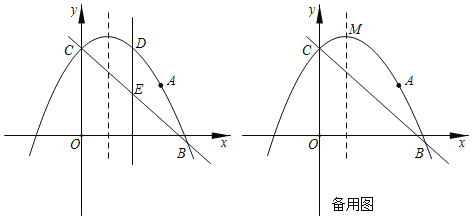
(1)求抛物线的解析式;
(2)点D为抛物线上位于直线![]() 上方的一点,过点D作
上方的一点,过点D作![]() 轴交直线
轴交直线![]() 于点E,点P为对称轴上一动点,当线段
于点E,点P为对称轴上一动点,当线段![]() 的长度最大时,求
的长度最大时,求![]() 的最小值;
的最小值;
(3)设点M为抛物线的顶点,在y轴上是否存在点Q,使![]() ?若存在,求点Q的坐标;若不存在,请说明理由.
?若存在,求点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是为(0,3)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.

(1)若抛物线过点C、A、A′,求此抛物线的解析式;
(2)求平行四边形ABOC和平行四边形A′B′OC′重叠部分△OC′D的周长;
(3)点M是第一象限内抛物线上的一动点,问:点M在何处时;△AMA′的面积最大?最大面积是多少?并求出此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备购进![]() 两种商品,
两种商品,![]() 种商品毎件的进价比
种商品毎件的进价比![]() 种商品每件的进价多20元,用3000元购进
种商品每件的进价多20元,用3000元购进![]() 种商品和用1800元购进
种商品和用1800元购进![]() 种商品的数量相同.商店将
种商品的数量相同.商店将![]() 种商品每件的售价定为80元,
种商品每件的售价定为80元,![]() 种商品每件的售价定为45元.
种商品每件的售价定为45元.
(1)![]() 种商品每件的进价和
种商品每件的进价和![]() 种商品每件的进价各是多少元?
种商品每件的进价各是多少元?
(2)商店计划用不超过1560元的资金购进![]() 两种商品共40件,其中
两种商品共40件,其中![]() 种商品的数量不低于
种商品的数量不低于![]() 种商品数量的一半,该商店有几种进货方案?
种商品数量的一半,该商店有几种进货方案?
(3)端午节期间,商店开展优惠促销活动,决定对每件![]() 种商品售价优惠
种商品售价优惠![]() (
(![]() )元,
)元,![]() 种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.
种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() (a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②
(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②![]() >4a,③0<b<1,④当x>﹣1时,y>0,其中正确结论的个数是( )
>4a,③0<b<1,④当x>﹣1时,y>0,其中正确结论的个数是( )
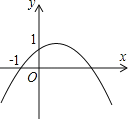
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党中央提出的“惠民政策”,我市今年计划开发建设A、B两种户型的“廉租房”共40套.投入资金不超过200万元,又不低于198万元.开发建设办公室预算:一套A型“廉租房”的造价为5.2万元,一套B型“廉租房”的造价为4.8万元.
(1)请问有几种开发建设方案?
(2)哪种建设方案投入资金最少?最少资金是多少万元?
(3)在(2)的方案下,为了让更多的人享受到“惠民”政策,开发建设办公室决定通过缩小“廉租房”的面积来降低造价、节省资金.每套A户型“廉租房”的造价降低0.7万元,每套B户型“廉租房”的造价降低0.3万元,将节省下来的资金全部用于再次开发建设缩小面积后的“廉租房”,如果同时建设A、B两种户型,请你直接写出再次开发建设的方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com