
【题目】如图,抛物线![]() 过点
过点![]() ,且与直线
,且与直线![]() 交于B、C两点,点B的坐标为
交于B、C两点,点B的坐标为![]() .
.
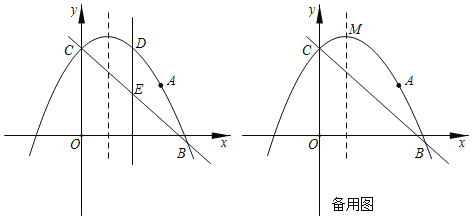
(1)求抛物线的解析式;
(2)点D为抛物线上位于直线![]() 上方的一点,过点D作
上方的一点,过点D作![]() 轴交直线
轴交直线![]() 于点E,点P为对称轴上一动点,当线段
于点E,点P为对称轴上一动点,当线段![]() 的长度最大时,求
的长度最大时,求![]() 的最小值;
的最小值;
(3)设点M为抛物线的顶点,在y轴上是否存在点Q,使![]() ?若存在,求点Q的坐标;若不存在,请说明理由.
?若存在,求点Q的坐标;若不存在,请说明理由.
【答案】(1)抛物线的解析式![]() ;(2)
;(2)![]() 的最小值为
的最小值为![]() ;(3)点Q的坐标:
;(3)点Q的坐标:![]() 、
、![]() .
.
【解析】
(1)将点B的坐标为![]() 代入
代入![]() ,
,![]() ,B的坐标为
,B的坐标为![]() ,将
,将![]() ,
,![]() 代入
代入![]() ,解得
,解得![]() ,
,![]() ,因此抛物线的解析式
,因此抛物线的解析式![]() ;
;
(2)设![]() ,则
,则![]() ,
,![]() ,当
,当![]() 时,
时,![]() 有最大值为2,此时
有最大值为2,此时![]() ,作点A关于对称轴的对称点
,作点A关于对称轴的对称点![]() ,连接
,连接![]() ,与对称轴交于点P.
,与对称轴交于点P.![]() ,此时
,此时![]() 最小;
最小;
(3)作![]() 轴于点H,连接
轴于点H,连接![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,由
,由![]() ,
,![]() ,可得
,可得![]() ,
,![]() 因为
因为![]() ,
,![]() ,所以
,所以![]() ,可知
,可知![]() 外接圆的圆心为H,于是
外接圆的圆心为H,于是![]() 设
设![]() ,则
,则![]() ,
,![]() 或
或![]() ,求得符合题意的点Q的坐标:
,求得符合题意的点Q的坐标:![]() 、
、![]() .
.
解:(1)将点B的坐标为![]() 代入
代入![]() ,
,
![]() ,
,
∴B的坐标为![]() ,
,
将![]() ,
,![]() 代入
代入![]() ,
,
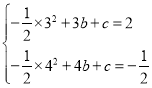
解得![]() ,
,![]() ,
,
∴抛物线的解析式![]() ;
;
(2)设![]() ,则
,则![]() ,
,
![]() ,
,
∴当![]() 时,
时,![]() 有最大值为2,
有最大值为2,
此时![]() ,
,
作点A关于对称轴的对称点![]() ,连接
,连接![]() ,与对称轴交于点P.
,与对称轴交于点P.

![]() ,此时
,此时![]() 最小,
最小,
∵![]() ,
,
∴![]() ,
,
![]() ,
,
即![]() 的最小值为
的最小值为![]() ;
;
(3)作![]() 轴于点H,连接
轴于点H,连接![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,

∵抛物线的解析式![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]()
∵![]() ,
,
![]() ,
,
∴![]() ,
,
可知![]() 外接圆的圆心为H,
外接圆的圆心为H,
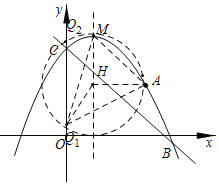
∴![]()
设![]() ,
,
则![]() ,
,
![]() 或
或![]()
∴符合题意的点Q的坐标:![]() 、
、![]() .
.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
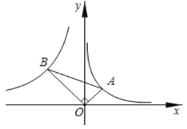
【题目】如图,Rt△AOB中,∠AOB=90°,顶点A,B分别在反比例函数y=![]() (x>0)与y=
(x>0)与y=![]() (x<0)的图象上,则tan∠BAO的值为 ____.
(x<0)的图象上,则tan∠BAO的值为 ____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=2x2+4x+k﹣1(k为大于2的正整数)与x轴有交点.
(1)求k的值及抛物线y=2x2+4x+k﹣1的对称轴;
(2)将抛物线y=2x2+4x+k﹣1在直线y=2上方的部分沿直线y=2翻折,其余部分不变,得到一个新图象,当直线y=![]() x+b与此图象有两个公共点时,求b的取值范围.
x+b与此图象有两个公共点时,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红树林学校在七年级新生中举行了全员参加的“防溺水”安全知识竞赛,试卷题目共10题,每题10分.现分别从三个班中各随机取10名同学的成绩(单位:分),收集数据如下:
1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
分数 人数 班级 | 60 | 70 | 80 | 90 | 100 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 |
| 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
分析数据:
平均数 | 中位数 | 众数 | |
1班 | 83 | 80 | 80 |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
根据以上信息回答下列问题:
(1)请直接写出表格中![]() 的值;
的值;
(2)比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由;
(3)为了让学生重视安全知识的学习,学校将给竞赛成绩满分的同学颁发奖状,该校七年级新生共570人,试估计需要准备多少张奖状?
查看答案和解析>>
科目:初中数学 来源: 题型:
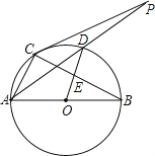
【题目】 如图,圆O是以AB为直径的△ABC的外接圆,D是劣弧![]() 的中点,连AD并延长与过C点的切线交于点P,OD与BC相交于E;
的中点,连AD并延长与过C点的切线交于点P,OD与BC相交于E;
(1)求证:OE=![]() AC;
AC;
(2)求证:![]() ;
;
(3)当AC=6,AB=10时,求切线PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
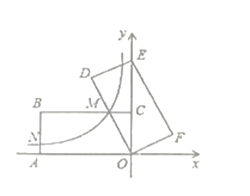
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 分别在
分别在![]() 轴的负半轴、
轴的负半轴、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在第二象限.将矩形
在第二象限.将矩形![]() 绕点
绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 落在
落在![]() 轴上,得到矩形
轴上,得到矩形![]() 与
与![]() 相交于点
相交于点![]() .若经过点
.若经过点![]() 的反比例函数
的反比例函数![]() 的图象交
的图象交![]() 于点
于点![]() 的图象交
的图象交![]() 于点
于点![]()
![]() 则
则![]() 的长为____.
的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,随着生活水平的提高,人们对饮水品质的需求越来越高.孝感市槐荫公司根据市场需求代理![]() 、
、![]() 两种型号的净水器,每台
两种型号的净水器,每台![]() 型净水器比每台
型净水器比每台![]() 型净水器进价多200元,用5万元购进
型净水器进价多200元,用5万元购进![]() 型净水器与用4.5万元购进
型净水器与用4.5万元购进![]() 型净水器的数量相等.
型净水器的数量相等.
(1)求每台![]() 型、
型、![]() 型净水器的进价各是多少元;
型净水器的进价各是多少元;
(2)槐荫公司计划购进![]() 、
、![]() 两种型号的净水器共50台进行试销,其中
两种型号的净水器共50台进行试销,其中![]() 型净水器为
型净水器为![]() 台,购买资金不超过9.8万元.试销时
台,购买资金不超过9.8万元.试销时![]() 型净水器每台售价2500元,
型净水器每台售价2500元,![]() 型净水器每台售价2180元.槐荫公司决定从销售
型净水器每台售价2180元.槐荫公司决定从销售![]() 型净水器的利润中按每台捐献
型净水器的利润中按每台捐献![]() 元作为公司帮扶贫困村饮水改造资金,设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为
元作为公司帮扶贫困村饮水改造资金,设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点D是AB的中点,点P是直线BC上一点,将△BDP沿DP所在的直线翻折后,点B落在B1处,若B1D⊥BC,则点P与点B之间的距离为( )
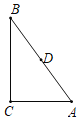
A.1B.![]() C.1或 3D.
C.1或 3D.![]() 或5
或5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com