
【题目】“绿水青山就是金山银山”,随着生活水平的提高,人们对饮水品质的需求越来越高.孝感市槐荫公司根据市场需求代理![]() 、
、![]() 两种型号的净水器,每台
两种型号的净水器,每台![]() 型净水器比每台
型净水器比每台![]() 型净水器进价多200元,用5万元购进
型净水器进价多200元,用5万元购进![]() 型净水器与用4.5万元购进
型净水器与用4.5万元购进![]() 型净水器的数量相等.
型净水器的数量相等.
(1)求每台![]() 型、
型、![]() 型净水器的进价各是多少元;
型净水器的进价各是多少元;
(2)槐荫公司计划购进![]() 、
、![]() 两种型号的净水器共50台进行试销,其中
两种型号的净水器共50台进行试销,其中![]() 型净水器为
型净水器为![]() 台,购买资金不超过9.8万元.试销时
台,购买资金不超过9.8万元.试销时![]() 型净水器每台售价2500元,
型净水器每台售价2500元,![]() 型净水器每台售价2180元.槐荫公司决定从销售
型净水器每台售价2180元.槐荫公司决定从销售![]() 型净水器的利润中按每台捐献
型净水器的利润中按每台捐献![]() 元作为公司帮扶贫困村饮水改造资金,设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为
元作为公司帮扶贫困村饮水改造资金,设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() 型净水器每台进价2000元,
型净水器每台进价2000元,![]() 型净水器每台进价1800元.(2)
型净水器每台进价1800元.(2)![]() 的最大值是
的最大值是![]() 元.
元.
【解析】(1)设A型净水器每台的进价为m元,则B型净水器每台的进价为(m-200)元,根据数量=总价÷单价结合用5万元购进A型净水器与用4.5万元购进B型净水器的数量相等,即可得出关于m的分式方程,解之经检验后即可得出结论;
(2)根据购买资金=A型净水器的进价×购进数量+B型净水器的进价×购进数量结合购买资金不超过9.8万元,即可得出关于x的一元一次不等式,解之即可得出x的取值范围,由总利润=每台A型净水器的利润×购进数量+每台B型净水器的利润×购进数量-a×购进A型净水器的数量,即可得出W关于x的函数关系式,再利用一次函数的性质即可解决最值问题.
(1)设A型净水器每台的进价为m元,则B型净水器每台的进价为(m-200)元,
根据题意得:![]() ,
,
解得:m=2000,
经检验,m=2000是分式方程的解,
∴m-200=1800.
答:A型净水器每台的进价为2000元,B型净水器每台的进价为1800元.
(2)根据题意得:2000x+1800(50-x)≤98000,
解得:x≤40.
W=(2500-2000)x+(2180-1800)(50-x)-ax=(120-a)x+19000,
∵当70<a<80时,120-a>0,
∴W随x增大而增大,
∴当x=40时,W取最大值,最大值为(120-a)×40+19000=23800-40a,
∴W的最大值是(23800-40a)元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】2016年3月,我市某中学举行了“爱我中国朗诵比赛”活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.根据图中提供的信息,回答下列问题:
(1)参加朗诵比赛的学生共有 人,并把条形统计图补充完整;
(2)扇形统计图中,m= ,n= ;C等级对应扇形有圆心角为 度;
(3)学校欲从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
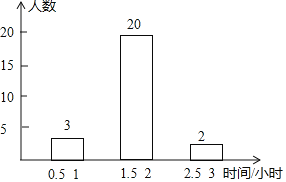
【题目】某校七年级开展了为期一周的“敬老爱亲”社会活动,并根据学生做家务的时间来评价他们在活动中的表现,学校随机抽查了部分学生在这次活动中做家务的时间,并绘制了如下的频数分布表和频数分布直方图.请根据图表中提供的信息,解答下列问题:
等级 | 做家务时间(小时) | 频数 | 百分比 |
A | 0.5≤x<1 | 3 | 6% |
B | 1<x<1.5 | a | 30% |
C | 1.5≤x<2 | 20 | 40% |
D | 2≤x<2.5 | b | m |
E | 2.5≤x<3 | 2 | 4% |
(1)这次活动中抽查的学生有______人,表中a=______,b=______,m=______,并补全频数分布直方图;
(2)若该校七年级有700名学生,请估计这所学校七年级学生一周做家务时间不足2小时而又不低于1小时的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“五一”黄金周期间,小明、小亮等同学随家人一同到西安华山游玩,如图是购买门票时,小明与他爸的对话,问题:
(1)小明他们一共去了几个成人?几个学生?
(2)请你帮小明算一算,用哪种方式买票更省钱?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2开始的连续偶数相加,它们和的情况如下表:
加数的个数(n) | 和(S) |
1 | 2=1×2 |
2 | 2+4=6=2×3 |
3 | 2+4+6=12=3×4 |
4 | 2+4+6+8=20=4×5 |
5 | 2+4+6+8+10=30=5×6 |
… | … |
(1)根据表中的规律,直接写出2+4+6+8+10+12+14=________
(2)根据表中的规律猜想:S=2+4+6+8+…+2n=___________(用n的代数式表示);
(3)利用上题中的公式计算102+104+106+…+200的值(要求写出计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(4,0),B(0,3),C(4,3),I是△ABC的内心,将△ABC绕原点逆时针旋转90°后,I的对应点I'的坐标为( )
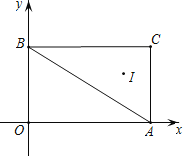
A. (﹣2,3) B. (﹣3,2) C. (3,﹣2) D. (2,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
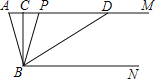
【题目】如图,已知AM∥BN,∠A=80°,点P是射线AM上动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于C、D.
(1)求∠CBD的度数;
(2)当点P运动时,那么∠APB:∠ADB的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com