
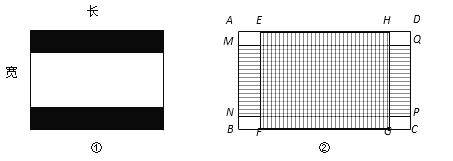
【题目】如图①,老旧电视机屏幕的长宽比为4︰3,但是多数电影图像的长宽比为2.4︰1,故在播放电影时电视机屏幕的上方和下方会有两条等宽的黑色带子.
(1)若图①中电视机屏幕为20寸(即屏幕对角线长度):
①该屏幕的长= 寸,宽= 寸;
②已知“屏幕浪费比=黑色带子的总面积:电视机屏幕的总面积”,求该电视机屏幕的浪费比.
(2) 为了兼顾电影的收视需求,一种新的屏幕的长宽比诞生了.如图②,这种屏幕(矩形ABCD)恰好包含面积相等且长宽比分别为4︰3的屏幕(矩形EFGH)与2.4︰1的屏幕(矩形MNPQ).求这种屏幕的长宽比.(参考数据:![]() ≈2.2,结果精确到0.1)
≈2.2,结果精确到0.1)
【答案】(1)①16 ,12,②![]() ;(2)1.8
;(2)1.8
【解析】
(1)①根据电视机屏幕的长宽比为4:3,设长为4x,则宽为3x,再由勾股定理求出x的值,进而可得出结论;
②设在该屏幕上播放长宽比为2.4:1的视频时,视频的宽为a寸(长为16寸),求出a的值,得出黑色带子的宽度,进而得出其比值;
(2)根据题意得出![]() ,得到
,得到![]() ,再由S矩形EFGH=S矩形MNPQ,即可得到
,再由S矩形EFGH=S矩形MNPQ,即可得到![]() ,进而可得出结论.
,进而可得出结论.
解:(1)①∵电视机屏幕的长宽比为4:3,
∴设长为4x,则宽为3x,
∵电视机屏幕为20寸,
∴![]() ,解得x=4,
,解得x=4,
∴4x=16,3x=12,
∴该屏幕的长为16寸,宽为12寸;
故答案为:16;12.
②设在该屏幕上播放长宽比为2.4︰1的视频时,视频的宽为a寸(长为16寸).
![]() ,解得 a=
,解得 a=![]() .所以黑色带子的宽的和=12-
.所以黑色带子的宽的和=12-![]() =
=![]() .
.
所以屏幕浪费比=
(2)由题意:![]() ,得:PQ=
,得:PQ=![]() BC,FG=
BC,FG=![]() EF.
EF.
因为S矩形EFGH=S矩形MNPQ,所以BC·![]() BC= EF·
BC= EF·![]() EF.
EF.
所以![]() ,∴
,∴![]() =
=![]() ≈1.8.答:这种屏幕的长宽比约为1.8
≈1.8.答:这种屏幕的长宽比约为1.8


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
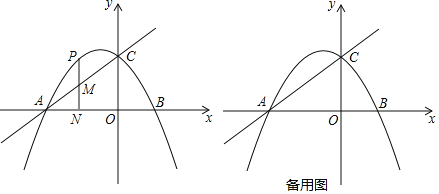
【题目】如图,已知直线![]() 交x轴负半轴于点A,交y轴于点C,抛物线
交x轴负半轴于点A,交y轴于点C,抛物线![]() 经过点A、C,与x轴的另一交点为B.
经过点A、C,与x轴的另一交点为B.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 设抛物线上任一动点P的横坐标为m.
设抛物线上任一动点P的横坐标为m.
①若点P在第二象限抛物线上运动,过P作![]() 轴于点N交直线AC于点M,当直线AC把线段PN分成2:3两部分时,求m的值;
轴于点N交直线AC于点M,当直线AC把线段PN分成2:3两部分时,求m的值;
②连接CP,以点P为直角顶点作等腰直角三角形CPQ,当点Q落在抛物线的对称轴上时,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“天空之城”摩天轮,位于宁波市杭州湾新区欢乐世界.摩天轮高约126米(最高点到地面的距离).如图,点O是摩天轮的圆心,AB是其垂直于地面的直径,小明在地面C处用测角仪测得摩天轮最高点A的仰角为45°,测得圆心O的仰角为30°,求摩天轮的半径.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校初二学生每周上网的时间,两位学生进行了抽样调查.小丽调查了初二电脑爱好者中40名学生每周上网的时间;小杰从全校400名初二学生中随机抽取了40名学生,调查了每周上网的时间.小丽与小杰整理各自样本数据,如下表所示:
时间段 (小时/周) | 小丽抽样 人数 | 小杰抽样 人数 |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(每组可含最低值,不含最高值)

(1)你认为哪位同学抽取的样本不合理?请说明理由;
(2)根据合理抽取的样本,把上图中的频数分布直方图补画完整;
(3)专家建议每周上网2小时以上(含2小时)的同学应适当减少上网的时间,估计该校全体初二学生中有多少名同学应适当减少上网的时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点.请你添加一个条件,使四边形EFGH为矩形,应添加的条件是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是为(0,3)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.

(1)若抛物线过点C、A、A′,求此抛物线的解析式;
(2)求平行四边形ABOC和平行四边形A′B′OC′重叠部分△OC′D的周长;
(3)点M是第一象限内抛物线上的一动点,问:点M在何处时;△AMA′的面积最大?最大面积是多少?并求出此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学团委组织征文活动,并设立若干奖项.学校计划派人根据设奖情况去购买![]() 三种奖品共
三种奖品共![]() 件,其中
件,其中![]() 型奖品件数比
型奖品件数比![]() 型奖品件数的
型奖品件数的![]() 倍少
倍少![]() 件,
件,![]() 型奖品所花费用不超过
型奖品所花费用不超过![]() 型奖品所花费用的
型奖品所花费用的![]() 倍.各种奖品的单价如右表所示.如果计划
倍.各种奖品的单价如右表所示.如果计划![]() 型奖品买
型奖品买![]() 件,买
件,买![]() 件奖品的总费用是
件奖品的总费用是![]() 元.
元.
|
|
| |
单价(元) |
|
|
|
(1)试求![]() 与
与![]() 之间的函数关系式,并求出自变量
之间的函数关系式,并求出自变量![]() 的取值范围;
的取值范围;
(2)请你设计一种方案,使得购买这三种奖品所花的总费用最少,并求出最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E是AD边中点,BD、CE交于点H,BE、AH交于点G,则下列结论:
①AG⊥BE;②BG=4GE;③S△BHE=S△CHD;④∠AHB=∠EHD.
其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com