
【题目】“天空之城”摩天轮,位于宁波市杭州湾新区欢乐世界.摩天轮高约126米(最高点到地面的距离).如图,点O是摩天轮的圆心,AB是其垂直于地面的直径,小明在地面C处用测角仪测得摩天轮最高点A的仰角为45°,测得圆心O的仰角为30°,求摩天轮的半径.(结果保留根号)

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字1、2、3、4,另有一个可以自由旋转的圆盘.被分成面积相等的3个扇形区,分别标有数字1、2、3(如图所示).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去;否则小亮去.
(1)用树状图或列表法求出小颖参加比赛的概率;
(2)你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏规则,使游戏公平.

查看答案和解析>>
科目:初中数学 来源: 题型:
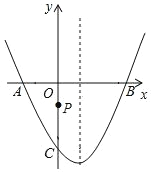
【题目】如图,在平面直角坐标系中,二次函数 y=ax2+bx+c 的图象交 x 轴于A、B 两点,交 y 轴于 C 点,P 为 y 轴上的一个动点,已知 A(﹣2,0)、C(0,﹣2![]() ),且抛物线的对称轴是直线 x=1.
),且抛物线的对称轴是直线 x=1.
(1)求此二次函数的解析式;
(2)连接 PB,则 ![]() PC+PB 的最小值是 ;
PC+PB 的最小值是 ;
(3)连接 PA、PB,P 点运动到何处时,使得∠APB=60°,请求出 P 点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线l:
中,直线l:![]() 与直线
与直线![]() ,直线
,直线![]() 分别交于点A,B,直线
分别交于点A,B,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(1)求直线![]() 与
与![]() 轴的交点坐标;
轴的交点坐标;
(2)横、纵坐标都是整数的点叫做整点.记线段![]() 围成的区域(不含边界)为
围成的区域(不含边界)为![]() .
.
①当![]() 时,结合函数图象,求区域
时,结合函数图象,求区域![]() 内的整点个数;
内的整点个数;
②若区域![]() 内没有整点,直接写出
内没有整点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系中,![]() 的边
的边![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在第二象限,且
在第二象限,且![]() ,
,![]() ,
,![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,并与
,并与![]() 轴交于点
轴交于点![]() ,点
,点![]() 在抛物线的对称轴上.
在抛物线的对称轴上.
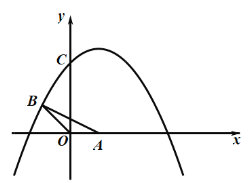
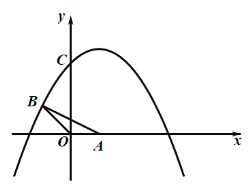
(图1) (备用图)
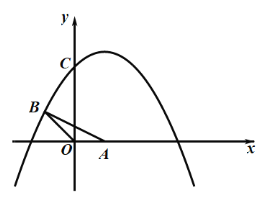
(备用图)
(1)求![]() 、
、![]() 的值,及抛物线的对称轴.
的值,及抛物线的对称轴.
(2)求证:以点![]() 为圆心,半径为
为圆心,半径为![]() 的圆与边
的圆与边![]() 相切.
相切.
(3)若满足条件![]() 与
与![]() 的点
的点![]() 恰好在抛物线上,请求出此时点
恰好在抛物线上,请求出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,
,![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 为抛物线的顶点,
为抛物线的顶点,![]() 轴于点
轴于点![]() ,且
,且![]() .
.

(1)求抛物线的解析式;
(2)做点![]() 与
与![]() 点关于对称轴对称,连接
点关于对称轴对称,连接![]() ,过点
,过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 是第一象限内抛物线上一点,连接
是第一象限内抛物线上一点,连接![]() 与
与![]() 相交于点
相交于点![]() ,过点
,过点![]() 做
做![]() 轴于点
轴于点![]() ,
,![]() 与
与![]() 相交于
相交于![]() ,连接
,连接![]() ,若
,若![]() ,求
,求![]() 点的坐标和
点的坐标和![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,老旧电视机屏幕的长宽比为4︰3,但是多数电影图像的长宽比为2.4︰1,故在播放电影时电视机屏幕的上方和下方会有两条等宽的黑色带子.
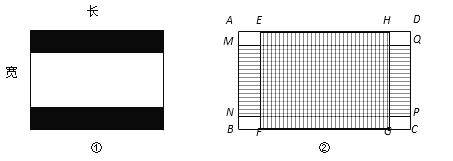
(1)若图①中电视机屏幕为20寸(即屏幕对角线长度):
①该屏幕的长= 寸,宽= 寸;
②已知“屏幕浪费比=黑色带子的总面积:电视机屏幕的总面积”,求该电视机屏幕的浪费比.
(2) 为了兼顾电影的收视需求,一种新的屏幕的长宽比诞生了.如图②,这种屏幕(矩形ABCD)恰好包含面积相等且长宽比分别为4︰3的屏幕(矩形EFGH)与2.4︰1的屏幕(矩形MNPQ).求这种屏幕的长宽比.(参考数据:![]() ≈2.2,结果精确到0.1)
≈2.2,结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
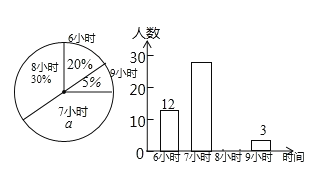
【题目】为了了解某校初中各年级学生每天的平均睡眠时间(单位:h,精确到1h),抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中百分数a的值为 ,所抽查的学生人数为 .
(2)求出平均睡眠时间为8小时的人数,并补全频数直方图.
(3)求出这部分学生的平均睡眠时间的众数和平均数.
(4)如果该校共有学生1200名,请你估计睡眠不足(少于8小时)的学生数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com