
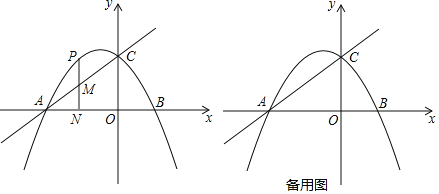
����Ŀ����ͼ����ֱ֪��![]() ��x�Ḻ�����ڵ�A����y���ڵ�C��������
��x�Ḻ�����ڵ�A����y���ڵ�C��������![]() ������A��C����x�����һ����ΪB��
������A��C����x�����һ����ΪB��
![]() �������ߵĽ���ʽ��
�������ߵĽ���ʽ��
![]() ������������һ����P�ĺ�����Ϊm��
������������һ����P�ĺ�����Ϊm��
������P�ڵڶ��������������˶�����P��![]() ���ڵ�N��ֱ��AC�ڵ�M����ֱ��AC���߶�PN�ֳ�2��3������ʱ����m��ֵ��
���ڵ�N��ֱ��AC�ڵ�M����ֱ��AC���߶�PN�ֳ�2��3������ʱ����m��ֵ��
������CP���Ե�PΪֱ�Ƕ���������ֱ��������CPQ������Q���������ߵĶԳ�����ʱ����ֱ��д����P�����꣮
���𰸡�(1)![]() ��(1)��
��(1)��![]() ��
��![]() ����
����![]() ������Ϊ
������Ϊ![]() ��
��![]() ��
��![]() ��
��![]()
��������
��1������ֱ��![]() �������ύ�ڵ�A����C�������A����C���������κ�������ʽ���������
�������ύ�ڵ�A����C�������A����C���������κ�������ʽ���������
��2������P�����꣬��ʾ��PM��MN������ֱ��AC���߶�PN�ֳ�2��3�����֣����������������⼴�ɣ�
�ڸ��ݡ�CPQ�ǵ��������Σ���![]() ��
��![]() ����
����![]() ����P�����꣬��ʾ����K����G�����꣬����
����P�����꣬��ʾ����K����G�����꣬����![]() �������̽�����⼴�ɣ�
�������̽�����⼴�ɣ�
��1����![]() ʱ��
ʱ��![]() ����
����![]() ����
����![]() ʱ��
ʱ��![]() �����
�����![]() ����
����![]() ��
��
��![]() ��
��![]() ����
����![]() ��
��![]() �����
�����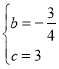 ��
��
![]() �����߽���ʽΪ
�����߽���ʽΪ![]() ��
��
��2������![]() ����
����![]() ��
��
![]() ��
��![]() ��
��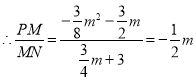 ��
��
![]() ֱ��AC���߶�PN�ֳ�2��3�����֣�
ֱ��AC���߶�PN�ֳ�2��3�����֣�
![]() ��
��![]() �����
�����![]() ��
��![]() ��
��
![]() ��
��![]() ����G���������ߵĶԳ�����K����ͼ��
����G���������ߵĶԳ�����K����ͼ��
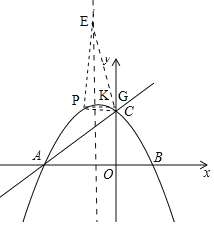
����ֱ��������CPQ��![]() ��
��![]()
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
��![]() �������ߵĶԳ���Ϊֱ��
�������ߵĶԳ���Ϊֱ��![]() ��
��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() ���ⷽ��
���ⷽ��![]() ��
��![]() ��
��![]() ��
��
�ⷽ��![]() ��
��![]() ��
��![]() ��
��
![]() ������Ϊ
������Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�ֱ��y��kx��k��0����˫����y��![]() ��x��0�����ڵ�A��2��n����
��x��0�����ڵ�A��2��n����
��1����n��k��ֵ��
��2����B��y���������ϵ�һ�㣬�ҡ�OAB�ǵ��������Σ���ֱ��д�����з��������ĵ�B�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ŀڴ���װ��4����ȫ��ͬ��С�ֱ��������1��2��3��4������һ������������ת��Բ�̣����ֳ������ȵ�3�����������ֱ��������1��2��3����ͼ��ʾ����Сӱ��С����ͨ����Ϸ������˭����ѧУ�μӸ�ӽ��������Ϸ����Ϊ��һ�˴ӿڴ�������һ��С����һ����ת��Բ�̣�����������ϵ�������Բ����ת������֮��С��4����ôСӱȥ������С��ȥ��
��1������״ͼ���б������Сӱ�μӱ����ĸ��ʣ�
��2������Ϊ����Ϸ��ƽ����˵�����ɣ�������ƽ�����ĸ���Ϸ����ʹ��Ϸ��ƽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
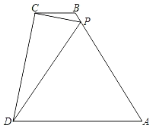
����Ŀ�� ��ͼ������ABCD�У�BC��AD��AB��AD��PΪ��AB��һ�㣬��PC��PD��CD��ֱ��CP�ҡ�CPD����A��BC��4BP����![]() ��_____��
��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��չ�ˡ�������ƽ�ȡ��ж�����г����ȡ������������ͻ��
5����������˳������飨ÿλͬѧֻѡȡ���ע��һ���������ݵ�������������������
����ͳ��ͼ������ͼ���ṩ����Ϣ������������⣺
��1����ε����ѧ�����ж�������
��2���뽫����ͳ��ͼ����������
��3��������ͳ��ͼ�С���ȡ���������ε�Բ�Ľ����� ���ȣ�
��4������Уѧ������Ϊ800�ˣ���������������������Ƹ�Уѧ���С��ж�����������
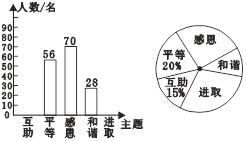
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
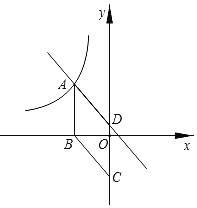
����Ŀ����ͼ����ֱ������ϵ�У�����ABCD�ı߳�Ϊ5�����Ϊ15����A��˫����y��![]() �ϣ���B��x���ϣ�C��D��y���ϣ�
�ϣ���B��x���ϣ�C��D��y���ϣ�
��1����A�������k��ֵ��
��2����ֱ��AD�Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB����O��ֱ������C��D����O�ϣ���E����O�⣬��EAC=��B=60�㣮
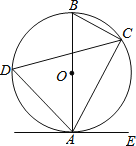
��1������ADC�Ķ�����
��2����֤��AE����O�����ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
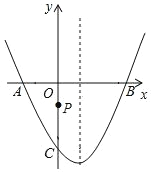
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ��� y��ax2+bx+c ��ͼ�� x ����A��B ���㣬�� y ���� C �㣬P Ϊ y ���ϵ�һ�����㣬��֪ A����2��0����C��0����2![]() �����������ߵĶԳ�����ֱ�� x��1��
�����������ߵĶԳ�����ֱ�� x��1��
(1)��˶��κ����Ľ���ʽ��
(2)���� PB���� ![]() PC+PB ����Сֵ�� ��
PC+PB ����Сֵ�� ��
(3)���� PA��PB��P ���˶����δ�ʱ��ʹ����APB��60��������� P �����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣��Ͼɵ��ӻ���Ļ�ij�����Ϊ4�U3�����Ƕ�����Ӱͼ��ij�����Ϊ2.4�U1�����ڲ��ŵ�Ӱʱ���ӻ���Ļ���Ϸ����·����������ȿ��ĺ�ɫ���ӣ�
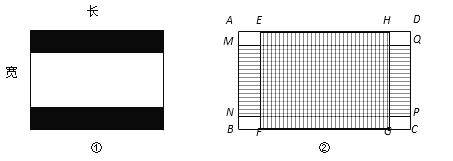
��1����ͼ���е��ӻ���ĻΪ20�磨����Ļ�Խ��߳��ȣ���
�ٸ���Ļ�ij��� �磬���� �磻
����֪����Ļ�˷ѱȣ���ɫ���ӵ�����������ӻ���Ļ�������������õ��ӻ���Ļ���˷ѱȣ�
��2�� Ϊ�˼�˵�Ӱ����������һ���µ���Ļ�ij����ȵ����ˣ���ͼ�ڣ�������Ļ������ABCD��ǡ�ð����������ҳ����ȷֱ�Ϊ4�U3����Ļ������EFGH����2.4�U1����Ļ������MNPQ������������Ļ�ij����ȣ����ο����ݣ�![]() ��2.2�������ȷ��0.1��
��2.2�������ȷ��0.1��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com