
【题目】在平面直角坐标系xOy中,直线y=kx(k≠0)与双曲线y=![]() (x>0)交于点A(2,n).
(x>0)交于点A(2,n).
(1)求n及k的值;
(2)点B是y轴正半轴上的一点,且△OAB是等腰三角形,请直接写出所有符合条件的点B的坐标.
【答案】(1)n=4,k=2;(2)点B的坐标为(0,8),(0,2![]() ),(0,
),(0,![]() ).
).
【解析】
(1)由点A的横坐标利用反比例函数图象上点的坐标特征可求出n值,进而可得出点A的坐标,由点A的坐标利用待定系数法可求出k值;
(2)分AB=AO,OA=OB,BO=BA三种情况考虑:①当AB=AO时,利用等腰三角形的性质可求出CB1的长度,结合点C的坐标可得出点B1的坐标;②当OA=OB时,由点A的坐标利用勾股定理可求出OA的长度,利用等腰三角形的性质可得出OB2的长度,进而可得出点B2的坐标;③当BO=BA时,设OB3=m,则CB3=4﹣m,AB3=m,在Rt△ACB3中利用勾股定理可得出关于m的方程,解之即可得出点B3的坐标.综上,此题得解.
(1)∵点A(2,n)在双曲线y=![]() 上,
上,
∴n=![]() =4,
=4,
∴点A的坐标为(2,4).
将A(2,4)代入y=kx,得:4=2k,
解得:k=2.
(2)分三种情况考虑,过点A作AC⊥y轴于点C,如图所示.
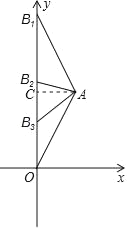
①当AB=AO时,CO=CB1=4,
∴点B1的坐标为(0,8);
②当OA=OB时,∵点A的坐标为(2,4),
∴OC=4,AC=2,
∴OA=![]() ,
,
∴OB2=2![]() ,
,
∴点B2的坐标为(0,2![]() );
);
③当BO=BA时,设OB3=m,则CB3=4﹣m,AB3=m,
在Rt△ACB3中,AB32=CB32+AC2,即m2=(4﹣m)2+22,
解得:m=![]() ,
,
∴点B3的坐标为(0,![]() ).
).
综上所述:点B的坐标为(0,8),(0,2![]() ),(0,
),(0,![]() ).
).


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】(1)如图1,将矩形ABCD折叠,使BC落在对角线BD上,折痕为BE,点C落在点C′处,若∠ADB=46°,则∠DBE的度数为 °.
(2)小明手中有一张矩形纸片ABCD,AB=4,AD=9.
(画一画)
如图2,点E在这张矩形纸片的边AD上,将纸片折叠,使AB落在CE所在直线上,折痕设为MN(点M,N分别在边AD,BC上),利用直尺和圆规画出折痕MN(不写作法,保留作图痕迹,并用黑色水笔把线段描清楚);
(算一算)
如图3,点F在这张矩形纸片的边BC上,将纸片折叠,使FB落在射线FD上,折痕为GF,点A,B分别落在点A′,B′处,若AG=![]() ,求B′D的长;
,求B′D的长;
(验一验)
如图4,点K在这张矩形纸片的边AD上,DK=3,将纸片折叠,使AB落在CK所在直线上,折痕为HI,点A,B分别落在点A′,B′处,小明认为B′I所在直线恰好经过点D,他的判断是否正确,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
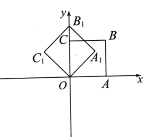
【题目】如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形![]() ,以此方式,绕点O旋转2018次得到正方形
,以此方式,绕点O旋转2018次得到正方形![]() ,如果点A的坐标为(1,0),那么那么点
,如果点A的坐标为(1,0),那么那么点![]() 的坐标为_____.
的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的小布袋中装有4个质地、大小完全相同的小球,它们分别标有数字0,1,2,3,小明从布袋里随机摸出一个小球,记下数字为![]() ,小红在剩下的3个小球中随机摸出一个小球,记下数字为
,小红在剩下的3个小球中随机摸出一个小球,记下数字为![]() ,这样确定了点
,这样确定了点![]() 的坐标
的坐标![]() .
.
(1)画树状图或列表,写出点![]() 所有可能的坐标;
所有可能的坐标;
(2)小明和小红约定做一个游戏,其规则为:若![]() 在第一象限,则小明胜;否则,小红胜;这个游戏公平吗?请你作出判断并说明理由.
在第一象限,则小明胜;否则,小红胜;这个游戏公平吗?请你作出判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD,两条对角线相交于O点,过点O作AC的垂线EF,分别交AD、BC于E、F点,连结CE,若OC![]() cm,CD=4cm,则DE的长为( )
cm,CD=4cm,则DE的长为( )
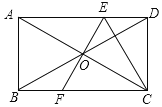
A.![]() cmB.5cmC.3cmD.2cm
cmB.5cmC.3cmD.2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们把横、纵坐标均为整数的点叫做整点,已知反比例函数y=![]() (m<0)与y=x2﹣5在第四象限内围成的封闭图形(包括边界)内的整点的个数为4,则实数m的取值范围为_____.
(m<0)与y=x2﹣5在第四象限内围成的封闭图形(包括边界)内的整点的个数为4,则实数m的取值范围为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y![]() x+b的图象与x轴,y轴分别交于A,B两点,与反比例函数y
x+b的图象与x轴,y轴分别交于A,B两点,与反比例函数y![]() (x<0)的图象交于点C(﹣2,2).
(x<0)的图象交于点C(﹣2,2).
(1)求一次函数与反比例函数的表达式;
(2)过点B作x轴的平行线交反比例函数的图象于点D,连接CD.求△BCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学实践活动课中小明同学测量某建筑物![]() 的高度,如图,已知斜坡
的高度,如图,已知斜坡![]() 的坡度为
的坡度为![]() ,小明在坡底点
,小明在坡底点![]() 处测得建筑物顶端
处测得建筑物顶端![]() 处的仰角为
处的仰角为![]() ,他沿着斜坡行走
,他沿着斜坡行走![]() 米到达点
米到达点![]() 处,在
处,在![]() 测得建筑 物顶端
测得建筑 物顶端![]() 处的仰角为
处的仰角为![]() ,小明和建筑物的剖面在同一平面内,小明的身高忽略不计.则建筑物的
,小明和建筑物的剖面在同一平面内,小明的身高忽略不计.则建筑物的![]() 高度约为( )(参考数据:
高度约为( )(参考数据:![]() )
)

A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
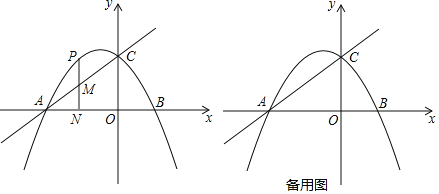
【题目】如图,已知直线![]() 交x轴负半轴于点A,交y轴于点C,抛物线
交x轴负半轴于点A,交y轴于点C,抛物线![]() 经过点A、C,与x轴的另一交点为B.
经过点A、C,与x轴的另一交点为B.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 设抛物线上任一动点P的横坐标为m.
设抛物线上任一动点P的横坐标为m.
①若点P在第二象限抛物线上运动,过P作![]() 轴于点N交直线AC于点M,当直线AC把线段PN分成2:3两部分时,求m的值;
轴于点N交直线AC于点M,当直线AC把线段PN分成2:3两部分时,求m的值;
②连接CP,以点P为直角顶点作等腰直角三角形CPQ,当点Q落在抛物线的对称轴上时,请直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com