
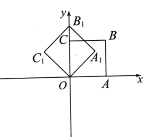
【题目】如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形![]() ,以此方式,绕点O旋转2018次得到正方形
,以此方式,绕点O旋转2018次得到正方形![]() ,如果点A的坐标为(1,0),那么那么点
,如果点A的坐标为(1,0),那么那么点![]() 的坐标为_____.
的坐标为_____.
【答案】(![]() ,0)
,0)
【解析】
根据图形可知:点B在以O为圆心,以OB为半径的圆上运动,由旋转可知:将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,相当于将线段OB绕点O逆时针旋转45°,可得对应点B的坐标,根据规律发现是8次一循环,可得结论.
∵四边形OABC是正方形,且OA=1,
∴B(1,1),
连接OB,
由勾股定理得:OB=![]() ,
,
由旋转得:OB=OB1=OB2=OB3=…=![]() ,
,
∵将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,
相当于将线段OB绕点O逆时针旋转45°,依次得到∠AOB=∠BOB1=∠B1OB2=…=45°,
∴B1(0,![]() ),B2(1,1),B3(
),B2(1,1),B3(![]() ,0),…,
,0),…,
发现是8次一循环,所以2019÷8=252…余3,
∴点B2019的坐标为(![]() ,0)
,0)
故答案为:(![]() ,0).
,0).


科目:初中数学 来源: 题型:
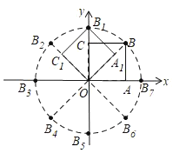
【题目】问题提出(1)如图①,在△ABC中,BC=6,D为BC上一点,AD=4,则△ABC面积的最大值是 .
问题探究(2)如图②,已知矩形ABCD的周长为12,求矩形ABCD面积的最大值.
问题解决(3)如图③,△ABC是葛叔叔家的菜地示意图,其中AB=30米,BC=40米,AC=50米,现在他想利用周边地的情况,把原来的三角形地拓展成符合条件的面积尽可能大、周长尽可能长的四边形地,用来建鱼塘.已知葛叔叔欲建的鱼塘是四边形ABCD,且满足∠ADC=60°.你认为葛叔叔的想法能否实现?若能,求出这个四边形鱼塘周长的最大值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列每个图形都是由一些黑点和一些白点按一定的规律组成的.
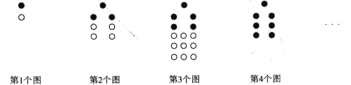
(1)根据规律,第4个图中有 个白点;第![]() 个图形中,白点和黑点总数的和为 (用
个图形中,白点和黑点总数的和为 (用![]() 表示,
表示,![]() 为正整数);
为正整数);
(2)有没有可能黑点比白点少2020个,如果有,求出此时![]() 的值;如果没有,请说明理由.
的值;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ACB=90°,AC=BC,CD平分∠ACB,点D,E关于CB对称,连接EB并延长,与AD的延长线交于点F,连接DE,CE.对于以下结论:
①DE垂直平分CB;②AD=BE;③∠F不一定是直角;④EF2+DF2=2CD2.
其中正确的是( )
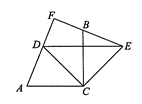
A.①④B.②③C.①③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
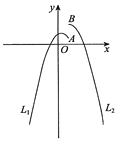
【题目】如图,函数y=-x2+![]() x+c(-2020≤x≤1)的图象记为L1,最大值为M1;函数y=-x2+2cx+1(1≤x≤2020)的图象记为L2,最大值为M2.L1的右端点为A,L2的左端点为B,L1,L2合起来的图形记为L.
x+c(-2020≤x≤1)的图象记为L1,最大值为M1;函数y=-x2+2cx+1(1≤x≤2020)的图象记为L2,最大值为M2.L1的右端点为A,L2的左端点为B,L1,L2合起来的图形记为L.
(1)当c=1时,求M1,M2的值;
(2)若把横、纵坐标都是整数的点称为“美点”,当点A,B重合时,求L上“美点”的个数;
(3)若M1,M2的差为![]() ,直接写出c的值.
,直接写出c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,且与
,且与![]() 轴交于点C
轴交于点C![]() ,与
,与![]() 轴交于A、B两点(点A在点B的右侧).
轴交于A、B两点(点A在点B的右侧).
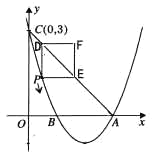
(1)求该抛物线的函数关系式;
(2)点P是该抛物线上一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥![]() 轴,交直线AC于点D;作PE∥x轴,交直线AC于点E,以PD,PE为边的矩形PEFD,问矩形PEFD周长是否存在最大值?若存在,求出此时P点的坐标及最大值;若不存在,请说明理由;
轴,交直线AC于点D;作PE∥x轴,交直线AC于点E,以PD,PE为边的矩形PEFD,问矩形PEFD周长是否存在最大值?若存在,求出此时P点的坐标及最大值;若不存在,请说明理由;
(3)在问题(2)的条件下,P点满足∠DAP=90°,且点E在![]() 轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在港口A的南偏东37°方向的海面上,有一巡逻艇B,A、B相距20海里,这时在巡逻艇的正北方向及港口A的北偏东67°方向上,有一渔船C发生故障.得知这一情况后,巡逻艇以25海里/小时的速度前往救援,问巡逻艇能否在1小时内到达渔船C处?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某社区今年准备新建一养老中心,其中规划建造三类养老专用房间共100间,这三类养老专用房间分别为单人间(1个养老床位),双人间(2个养老床位),三人间(3个养老床位),因实际需要,单人间房间数在10至30之间(包括10和30),且双人间的房间数是单人间的2倍,设规划建造单人间的房间数为![]() .
.
(1)根据题意,填写下表:
单人间的房间数 | 10 | … |
| … | 30 |
双人间的房间数 | _________ | … |
| … | 60 |
三人间的房间数 | 70 | … | _________ | … | _________ |
养老床位数 | 260 | … | _________ | … | _________ |
(2)若该养老中心建成后可提供养老床位200个,求![]() 的值;
的值;
(3)求该养老中心建成后最多提供养老床位多少个?最少提供养老床位多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com