
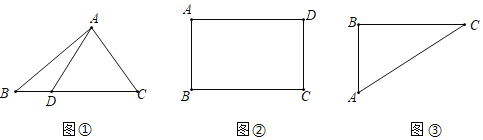
ЁОЬтФПЁПЮЪЬтЬсГіЃЈ1ЃЉШчЭМЂйЃЌдкЁїABCжаЃЌBCЃН6ЃЌDЮЊBCЩЯвЛЕуЃЌADЃН4ЃЌдђЁїABCУцЛ§ЕФзюДѓжЕЪЧЁЁ ЁЁЃЎ
ЮЪЬтЬНОПЃЈ2ЃЉШчЭМЂкЃЌвбжЊОиаЮABCDЕФжмГЄЮЊ12ЃЌЧѓОиаЮABCDУцЛ§ЕФзюДѓжЕЃЎ
ЮЪЬтНтОіЃЈ3ЃЉШчЭМЂлЃЌЁїABCЪЧИ№ЪхЪхМвЕФВЫЕиЪОвтЭМЃЌЦфжаABЃН30УзЃЌBCЃН40УзЃЌACЃН50УзЃЌЯждкЫћЯыРћгУжмБпЕиЕФЧщПіЃЌАбдРДЕФШ§НЧаЮЕиЭиеЙГЩЗћКЯЬѕМўЕФУцЛ§ОЁПЩФмДѓЁЂжмГЄОЁПЩФмГЄЕФЫФБпаЮЕиЃЌгУРДНЈгуЬСЃЎвбжЊИ№ЪхЪхгћНЈЕФгуЬСЪЧЫФБпаЮABCDЃЌЧвТњзуЁЯADCЃН60ЁуЃЎФуШЯЮЊИ№ЪхЪхЕФЯыЗЈФмЗёЪЕЯжЃПШєФмЃЌЧѓГіетИіЫФБпаЮгуЬСжмГЄЕФзюДѓжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ12ЃЛЃЈ2ЃЉ9ЃЛЃЈ3ЃЉФмЪЕЯжЃЛ170ЃЈУзЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЕБADЁЭBCЪБЃЌЁїABCЕФУцЛ§зюДѓЃЎ
ЃЈ2ЃЉгЩЬтвтОиаЮСкБпжЎКЭЮЊ6ЃЌЩшОиаЮЕФвЛБпЮЊmЃЌСэвЛБпЮЊ6ЉmЃЌПЩЕУSЃНmЃЈ6ЉmЃЉЃНЉЃЈmЉ3ЃЉ2+9ЃЌРћгУЖўДЮКЏЪ§ЕФаджЪНтОіЮЪЬтМДПЩЃЎ
ЃЈ3ЃЉгЩЬтвтЃЌACЃН100ЃЌЁЯADCЃН60ЁуЃЌМДЕуDдкгХЛЁADCЩЯдЫЖЏЃЌЕБЕуDдЫЖЏЕНгХЛЁADCЕФжаЕуЪБЃЌЫФБпаЮгуЬСУцЛ§КЭжмГЄДяЕНзюДѓжЕЃЌДЫЪБЁїACDЮЊЕШБпШ§НЧаЮЃЌМЦЫуГіЁїADCЕФУцЛ§КЭADЕФГЄМДПЩЕУГіетИіЫФБпаЮгуЬСУцЛ§КЭжмГЄЕФзюДѓжЕЃЎ
ЃЈ1ЃЉШчЭМЂйжаЃЌ
ЁпBCЃН6ЃЌADЃН4ЃЌ
ЁрЕБADЁЭBCЪБЃЌЁїABCЕФУцЛ§зюДѓЃЌзюДѓжЕЃН![]() ЁС6ЁС4ЃН12ЃЎ
ЁС6ЁС4ЃН12ЃЎ
ЙЪД№АИЮЊ12ЃЎ
ЃЈ2ЃЉЁпОиаЮЕФжмГЄЮЊ12ЃЌ
ЁрСкБпжЎКЭЮЊ6ЃЌЩшОиаЮЕФвЛБпЮЊmЃЌСэвЛБпЮЊ6ЉmЃЌ
ЁрSЃНmЃЈ6ЉmЃЉЃНЉЃЈmЉ3ЃЉ2+9ЃЌ
ЁпЉ1ЃМ0ЃЌ
ЁрmЃН3ЪБЃЌSгазюДѓжЕЃЌзюДѓжЕЮЊ9ЃЎ
ЃЈ3ЃЉШчЭМЂлжаЃЌ
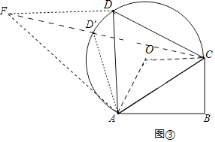
ЁпACЃН50УзЃЌABЃН40УзЃЌBCЃН30УзЃЌ
ЁрAC2ЃНAB2+BC2
ЁрЁЯABCЃН90ЁуЃЌ
зїЁїAOCЃЌЪЙЕУЁЯAOCЃН120ЁуЃЌOAЃНOCЃЌвдOЮЊдВаФЃЌOAГЄЮЊАыОЖЛЁбOЃЌ
ЁпЁЯADCЃН60ЁуЃЌ
ЁрЕуDдкгХЛЁADCЩЯдЫЖЏЃЌ
ЕБЕуDЪЧгХЛЁADCЕФжаЕуЪБЃЌЫФБпаЮABCDУцЛ§ШЁЕУзюДѓжЕЃЌ
ЩшDЁфЪЧгХЛЁADCЩЯШЮвтвЛЕуЃЌСЌНгADЁфЃЌCDЁфЃЌбгГЄCDЁфЕНFЃЌЪЙЕУDЁфFЃНDЁфAЃЌСЌНгAFЃЌдђЁЯAFCЃН30ЁуЃН![]() ЁЯADCЃЌ
ЁЯADCЃЌ
ЁрЕуFдкDЮЊдВаФDAЮЊАыОЖЕФдВЩЯЃЌ
ЁрDFЃНDAЃЌ
ЁпDF+DCЁнCFЃЌ
ЁрDA+DCЁнDЁфA+DЁфCЃЌ
ЁрDA+DC+ACЁнDЁфA+DЁфC+ACЃЌ
ЁрДЫЪБЫФБпаЮADCBЕФжмГЄзюДѓЃЌзюДѓжЕЃН40+30+50+50ЃН170ЃЈУзЃЉЃЎ
Д№ЃКетИіЫФБпаЮгуЬСжмГЄЕФзюДѓжЕЮЊ170ЃЈУзЃЉЃЎ


 зжДЪОфЦЊгыЭЌВНзїЮФДяБъЯЕСаД№АИ
зжДЪОфЦЊгыЭЌВНзїЮФДяБъЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2019Фъ4дТ15ШеАјЭэЗЈЙњЕиБъадНЈжўАЭРшЪЅФИдКЭЛдтДѓЛ№ЭЬЪЩЃЌЕМжТЮнЖЅКЭжїМтЫўЬЎЫњЃЌИчЬиЪНЕФУЕЙхЛЈДАЫ№ЛйЃЎЮЊСЫжиНЈАЭРшЪЅФИдКЃЌЩшМЦаЁзщЩшМЦСЫвЛИігЩШ§ЩЋВЃСЇЦДГЩЕФЛЈДАЃЌШчЭМЫљЪОЃЌжїЬхВПЗжгЩОиаЮ![]() КЭАыдВ
КЭАыдВ![]() зщГЩЃЌЩшАыдВ
зщГЩЃЌЩшАыдВ![]() ЮЊЧјгђ
ЮЊЧјгђ![]() ЃЌЫФИіШЋЕШЕФжБНЧШ§НЧаЮ
ЃЌЫФИіШЋЕШЕФжБНЧШ§НЧаЮ![]() ЮЊЧјгђ
ЮЊЧјгђ![]() ЃЌОиаЮФкЕФвѕгАВПЗжЮЊЧјгђ
ЃЌОиаЮФкЕФвѕгАВПЗжЮЊЧјгђ![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЌЩш
ЃЌЩш![]()
![]() ЕБ
ЕБ![]() ЃЌЧѓЧјгђ
ЃЌЧѓЧјгђ![]() ЕФУцЛ§ЃЎ
ЕФУцЛ§ЃЎ
![]() ЧыгУ
ЧыгУ![]() ЕФДњЪ§ЪНБэЪОГіЧјгђ
ЕФДњЪ§ЪНБэЪОГіЧјгђ![]() ЕФУцЛ§ВЂЧѓГіЦфзюДѓжЕЃЎ
ЕФУцЛ§ВЂЧѓГіЦфзюДѓжЕЃЎ
![]() ЮЊСЫУРЙлЃЌЩшжУЧјгђ
ЮЊСЫУРЙлЃЌЩшжУЧјгђ![]() гыЧјгђ
гыЧјгђ![]() ЕФУцЛ§жЎБШЮЊ
ЕФУцЛ§жЎБШЮЊ![]() ЃЎЧјгђ
ЃЎЧјгђ![]() ЁЂЧјгђ
ЁЂЧјгђ![]() ЁЂЧјгђ
ЁЂЧјгђ![]() ЗжБ№ЯтЧЖКьЁЂРЖЁЂЛЦЩЋШ§жжВЃСЇЃЌвбжЊетШ§жжВЃСЇЕФЕЅМлжЎКЭЮЊ
ЗжБ№ЯтЧЖКьЁЂРЖЁЂЛЦЩЋШ§жжВЃСЇЃЌвбжЊетШ§жжВЃСЇЕФЕЅМлжЎКЭЮЊ![]() дЊ(Ш§жжВЃСЇЕФЕЅМлОљЮЊећЪ§)ЃЌећИіЛЈДАЯтЧЖВЃСЇЙВЛЈЗбСЫ
дЊ(Ш§жжВЃСЇЕФЕЅМлОљЮЊећЪ§)ЃЌећИіЛЈДАЯтЧЖВЃСЇЙВЛЈЗбСЫ![]() дЊЃЌЧѓетШ§жжВЃСЇЕФЕЅМлЃЎ(
дЊЃЌЧѓетШ§жжВЃСЇЕФЕЅМлЃЎ(![]() ШЁ
ШЁ![]() )
)

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
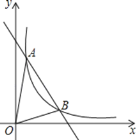
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§yЃНkx+bгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓНЛгкAЃЈmЃЌ6ЃЉЃЌBЃЈ3ЃЌnЃЉСНЕуЃЎ
ЕФЭМЯѓНЛгкAЃЈmЃЌ6ЃЉЃЌBЃЈ3ЃЌnЃЉСНЕуЃЎ
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉИљОнЭМЯѓжБНгаДГі![]() ЕФxЕФШЁжЕЗЖЮЇЃЛ
ЕФxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЧѓЁїAOBЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
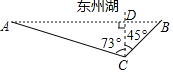
ЁОЬтФПЁПФГЪаЮЊСЫДДНЈТЬЩЋЩњЬЌГЧЪаЃЌдкГЧЖЋНЈСЫЁАЖЋжнКўЁБОАЧјЃЌаЁУїКЭаЁССЯыВтСПЁАЖЋжнКўЁБЖЋЮїСНЖЫAЁЂBМфЕФОрРыЃЎгкЪЧЃЌЫћУЧШЅСЫКўБпЃЌШчЭМЃЌдкКўЕФФЯАЖЕФЫЎЦНЕиУцЩЯЃЌбЁШЁСЫПЩжБНгЕНДяЕуBЕФвЛЕуCЃЌВЂВтЕУBCЃН350УзЃЌЕуAЮЛгкЕуCЕФББЦЋЮї73ЁуЗНЯђЃЌЕуBЮЛгкЕуCЕФББЦЋЖЋ45ЁуЗНЯђЃЎЧыФуИљОнвдЩЯЬсЙЉЕФаХЯЂЃЌМЦЫуЁАЖЋжнКўЁБЖЋЮїСНЖЫжЎМфABЕФГЄЃЎЃЈНсЙћОЋШЗЕН1УзЃЉЃЈВЮПМЪ§ОнЃКsin73ЁуЁж0.9563ЃЌcos73Ёж0.2924ЃЌtan73ЁуЁж3.2709ЃЌ![]() Ёж1.414ЃЎЃЉ
Ёж1.414ЃЎЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАЛДФЯХЃШтЬРЁБЪЧАВЛежЊУћЕиЗНаЁГдЃЎФГЗжЕъОРэЗЂЯжЃЌЕБУПЭыХЃШтЬРЕФЪлМлЮЊ6дЊЪБЃЌУПЬьФмТєГі500ЭыЃЛЕБУПЭыХЃШтЬРЕФЪлМлУПдіМг0.5дЊЪБЃЌУПЬьОЭЛсЩйТєГі20ЭыЃЌЩшУПЭыХЃШтЬРЕФЪлМлдіМг![]() дЊЪБЃЌвЛЬьЕФгЊвЕЖюЮЊ
дЊЪБЃЌвЛЬьЕФгЊвЕЖюЮЊ![]() дЊЃЎ
дЊЃЎ
ЃЈ1ЃЉЧѓ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЈВЛвЊЧѓаДГі
ЕФКЏЪ§ЙиЯЕЪНЃЈВЛвЊЧѓаДГі![]() ЕФШЁжЕЗЖЮЇЃЉЃЛ
ЕФШЁжЕЗЖЮЇЃЉЃЛ
ЃЈ2ЃЉПМТЧЕНЙЫПЭПЩНгЪмМлИё![]() дЊ/ЭыЕФЗЖЮЇЪЧ
дЊ/ЭыЕФЗЖЮЇЪЧ![]() ЃЌЧв
ЃЌЧв![]() ЮЊећЪ§ЃЌВЛПМТЧЦфЫћвђЫиЃЌдђИУЗжЕъЕФХЃШтЬРУПЭыЖрЩйдЊЪБЃЌУПЬьЕФХЃШтЬРгЊвЕЖюзюДѓЃПзюДѓгЊвЕЖюЪЧЖрЩйдЊЃП
ЮЊећЪ§ЃЌВЛПМТЧЦфЫћвђЫиЃЌдђИУЗжЕъЕФХЃШтЬРУПЭыЖрЩйдЊЪБЃЌУПЬьЕФХЃШтЬРгЊвЕЖюзюДѓЃПзюДѓгЊвЕЖюЪЧЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌЯв
жаЃЌЯв![]() гыЯв
гыЯв![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() ЕФжБЯпгы
ЕФжБЯпгы![]() ЕФбгГЄЯпНЛгкЕу
ЕФбгГЄЯпНЛгкЕу![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
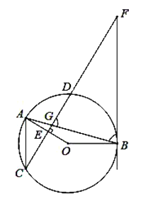
ЃЈ1ЃЉШє![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() ЪЧ
ЪЧ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌЧыгУ
ЃЌЧыгУ![]() БэЪО
БэЪО![]() ЕФАыОЖЃЛ
ЕФАыОЖЃЛ
ЃЈ3ЃЉЧѓжЄЃК![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌЕуFДгСтаЮABCDЕФЖЅЕуAГіЗЂЃЌбиAЁњDЁњBвд1cm/sЕФЫйЖШдШЫйдЫЖЏЕНЕуBЃЌЭМ2ЪЧЕуFдЫЖЏЪБЃЌЁїFBCЕФУцЛ§yЃЈcm2ЃЉЫцЪБМфxЃЈsЃЉБфЛЏЕФЙиЯЕЭМЯѓЃЌдђaЕФжЕЮЊЃЈЁЁЁЁЃЉ

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЁїABCЮЊЕШБпШ§НЧаЮЃЌЕуDЪЧЯпЖЮABЩЯвЛЕуЃЈВЛгыAЁЂBжиКЯЃЉЃЎНЋЯпЖЮCDШЦЕуCФцЪБеыа§зЊ60ЁуЕУЕНЯпЖЮCEЃЎСЌНсDEЁЂBEЃЎ
ЃЈ1ЃЉвРЬтвтВЙШЋЭМ1ВЂХаЖЯADгыBEЕФЪ§СПЙиЯЕЃЎ
ЃЈ2ЃЉЙ§ЕуAзїAFЁЭEBНЛEBбгГЄЯпгкЕуFЃЎгУЕШЪНБэЪОЯпЖЮEBЁЂDBгыAFжЎМфЕФЪ§СПЙиЯЕВЂжЄУїЃЎ
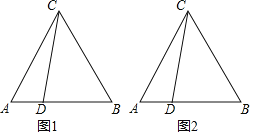
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com