
【题目】在一个不透明的小布袋中装有4个质地、大小完全相同的小球,它们分别标有数字0,1,2,3,小明从布袋里随机摸出一个小球,记下数字为![]() ,小红在剩下的3个小球中随机摸出一个小球,记下数字为
,小红在剩下的3个小球中随机摸出一个小球,记下数字为![]() ,这样确定了点
,这样确定了点![]() 的坐标
的坐标![]() .
.
(1)画树状图或列表,写出点![]() 所有可能的坐标;
所有可能的坐标;
(2)小明和小红约定做一个游戏,其规则为:若![]() 在第一象限,则小明胜;否则,小红胜;这个游戏公平吗?请你作出判断并说明理由.
在第一象限,则小明胜;否则,小红胜;这个游戏公平吗?请你作出判断并说明理由.
科目:初中数学 来源: 题型:
【题目】如图是二次函数![]() 图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(
图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(![]() ,y2)是抛物线上两点,则
,y2)是抛物线上两点,则
y1>y2.其中说法正确的是( )

A. ①② B. ②③ C. ①②④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2tx﹣t+1(是常数).
(1)求此函数的顶点坐标.(用含t的代数式表示)
(2)当x≥2时,y随x的增大而减小,求t的取值范围.
(3)当0≤x≤1时,该函数有最大值4,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,y=ax2+bx-2的图象过A(1,0),B(-2,0),与y轴交于点C.
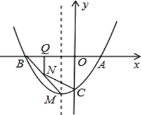
(1)求抛物线关系式及顶点M的坐标;
(2)若N为线段BM上一点,过N作x轴的垂线,垂足为Q,当N在线段BM上运动(N不与点B、点M重合),设NQ的长为t,四边形NQAC的面积为S,求S与t的关系式并求出S的最大值;
(3)在抛物线的对称轴上是否存在点P,使△PAC为直角三角形?若存在,请直接写出所有符合条件P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小芳给校方提供学生体育锻炼的情况报告,在校内对全校学生进行了抽样调查,每位学生只选择一项自己最喜欢的体育运动.其中,![]() 代表最喜欢参加兵乒球运动;
代表最喜欢参加兵乒球运动;![]() 代表最喜欢参加羽毛球运动;
代表最喜欢参加羽毛球运动;![]() 代表最喜欢气排球运动;
代表最喜欢气排球运动;![]() 代表最喜欢篮球运动,下图是她还未完成的条形统计图与扇形统计图,根据统计图所给出的信息,这个样本中最喜欢篮球运动(即
代表最喜欢篮球运动,下图是她还未完成的条形统计图与扇形统计图,根据统计图所给出的信息,这个样本中最喜欢篮球运动(即![]() )的百分率与人数是( )
)的百分率与人数是( )

A.24,26%B.33,26.4%C.28,22.4%D.25,23.6%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F分别是平行四边形ABCD的边AD、BC上的点,且BE∥DF,AC分别交BE、DF于点G、H.下列结论:①四边形BFDE是平行四边形;②△AGE≌△CHF;③BG=DH;④S△AGE:S△CDH=GE:DH,其中正确的个数是( )
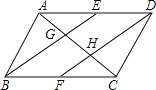
A.1B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=kx(k≠0)与双曲线y=![]() (x>0)交于点A(2,n).
(x>0)交于点A(2,n).
(1)求n及k的值;
(2)点B是y轴正半轴上的一点,且△OAB是等腰三角形,请直接写出所有符合条件的点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
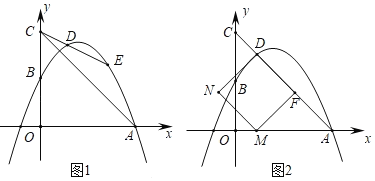
【题目】如图1,二次函数y![]() x2+bx+c的图象过A(5,0)和B(0,
x2+bx+c的图象过A(5,0)和B(0,![]() )两点,射线CE绕点C(0,5)旋转,交抛物线于D,E两点,连接AC.
)两点,射线CE绕点C(0,5)旋转,交抛物线于D,E两点,连接AC.
(1)求二次函数y![]() x2+bx+c的表达式;
x2+bx+c的表达式;
(2)连接OE,AE,当△CEO是以CO为底的等腰三角形时,求点E的坐标和△ACE的面积;
(3)如图2,射线CE旋转时,取DE的中点F,以DF为边作正方形DFMN.当点E和点A重合时,正方形DFMN的顶点M恰好落在x轴上.
①求点M的坐标;
②当点E和点A重合时,将正方形DFMN沿射线CE方向以每秒![]() 个单位长度平移.设运动时间为t秒.直接写出正方形DFMN落在x轴下方的面积S与时间t(0≤t≤4)的函数表达式.
个单位长度平移.设运动时间为t秒.直接写出正方形DFMN落在x轴下方的面积S与时间t(0≤t≤4)的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
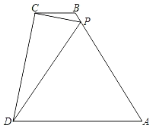
【题目】 如图,梯形ABCD中,BC∥AD,AB=AD,P为边AB上一点,连PC,PD,CD垂直于CP且∠CPD=∠A,BC=4BP,则![]() =_____.
=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com