
【题目】如图,y=ax2+bx-2的图象过A(1,0),B(-2,0),与y轴交于点C.
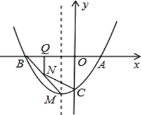
(1)求抛物线关系式及顶点M的坐标;
(2)若N为线段BM上一点,过N作x轴的垂线,垂足为Q,当N在线段BM上运动(N不与点B、点M重合),设NQ的长为t,四边形NQAC的面积为S,求S与t的关系式并求出S的最大值;
(3)在抛物线的对称轴上是否存在点P,使△PAC为直角三角形?若存在,请直接写出所有符合条件P的坐标.
【答案】(1)y=x2+x-2 ,顶点M的坐标是(-![]() ,-
,-![]() );(2)S与t间的函数关系式为S=-
);(2)S与t间的函数关系式为S=-![]() t2+
t2+![]() t+3,当t=
t+3,当t=![]() 时,S的最大值为
时,S的最大值为![]() ;(3)存在符合条件的点P,其坐标分别是:P1(-
;(3)存在符合条件的点P,其坐标分别是:P1(-![]() ,-
,-![]() ),P2(-
),P2(-![]() ,-
,-![]() ),P3(-
),P3(-![]() ,-
,-![]() ),P4(-
),P4(-![]() ,
,![]() ).
).
【解析】
(1)利用交点式得出抛物线的解析式为y=a(x-1)(x+2),将C(0,-2)坐标代入求出a的值即可;
(2)利用待定系数法求出线段BM所在的直线的解析式,再利用S=S△AOC+S梯形OCNQ求出S与t间的函数关系式即可求出最值;
(3)利用①若∠APC=90°,则PC2+PA2=AC2,②若∠ACP=90°,则PC2+AC2=PA2,③若∠PAC=90°,则AC2+PA2=PC2,分别求出m的值即可得出P点坐标.
解:(1)∵二次函数y=ax2+bx-2的图象经过点A(1,0)及B(-2,0)两点.
∴设抛物线的解析式为y=a(x-1)(x+2),
将C(0,-2)坐标代入,-2=a(0-1)(0+2),
解得:a=1,
故y=x2+x-2=(x+![]() )2-
)2-![]() ;
;
则其顶点M的坐标是(-![]() ,-
,-![]() );
);
(2)设线段BM所在直线的解析式为y=kx+b,
∴ 解得,
解得, ,
,
∴线段BM所在的直线的解析式为y=-![]() x-3,
x-3,
∵-t=-![]() x-3,
x-3,
∴x=![]() t-2,
t-2,
点N的坐标为N(![]() t-2,-t),
t-2,-t),
∴S=S△AOC+S梯形OCNQ=![]() ×1×2+
×1×2+![]() (2+t)|
(2+t)|![]() t-2|═-
t-2|═-![]() t2+
t2+![]() t+3,
t+3,
∴S与t间的函数关系式为S=-![]() t2+
t2+![]() t+3=-
t+3=-![]() (t-
(t-![]() )2+
)2+![]() ,
,
当t=![]() 时,S的最大值为
时,S的最大值为![]() ;
;
(3)存在符合条件的点P, 其坐标分别是:
P1(-![]() ,-
,-![]() ),P2(-
),P2(-![]() ,-
,-![]() ),P3(-
),P3(-![]() ,-
,-![]() ),P4(-
),P4(-![]() ,
,![]() ).
).
解答过程如下:
设点P的坐标为P(-![]() ,m),如图,连接PA,PC,作CE⊥MP于E.
,m),如图,连接PA,PC,作CE⊥MP于E.
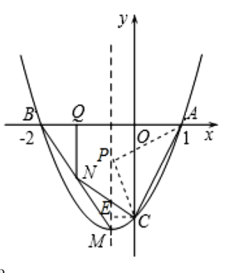
则AC2=12+22=5,
PA2=(-![]() -1)2+m2,PC2=(
-1)2+m2,PC2=(![]() )2+(m+2)2,
)2+(m+2)2,
分以下三种情况讨论:
①若∠APC=90°,则PC2+PA2=AC2,
即(-![]() -1)2+m2+(
-1)2+m2+(![]() )2+(m+2)2=5,
)2+(m+2)2=5,
解得:m1=-![]() ,m2=-
,m2=-![]() ,
,
②若∠ACP=90°,则PC2+AC2=PA2,
即(![]() )2+(m+2)2+5=(-
)2+(m+2)2+5=(-![]() -1)2+m2,
-1)2+m2,
解得:m=-![]() .
.
③若∠PAC=90°,则AC2+PA2=PC2,
即(-![]() -1)2+m2+5=(
-1)2+m2+5=(![]() )2+(m+2)2,
)2+(m+2)2,
解得:m=![]() ,
,
综上所述,存在满足条件的点P,其坐标分别是:P1(-![]() ,-
,-![]() ),P2(-
),P2(-![]() ,-
,-![]() ),P3(-
),P3(-![]() ,-
,-![]() ),P4(-
),P4(-![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,⊙O分别切AB于M,BC于N,连接BO、CO,BO=CO.

(1)求证:AC是⊙O的切线;
(2)连接MC,若![]() ,求sin∠B的值.
,求sin∠B的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
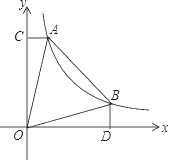
【题目】如图,A、B两点在反比例函数![]() (k>0,x>0)的图象上,AC⊥y轴于点C,BD⊥x轴于点D,点A的横坐标为a,点B的横坐标为b,且a<b.
(k>0,x>0)的图象上,AC⊥y轴于点C,BD⊥x轴于点D,点A的横坐标为a,点B的横坐标为b,且a<b.
(1)若△AOC的面积为4,求k值;
(2)若a=1,b=k,当AO=AB时,试说明△AOB是等边三角形;
(3)若OA=OB,证明:OC=OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=k1x+b交x轴于点A(-3,0),交y轴于点B(0,2),并与![]() 的图象在第一象限交于点C,CD⊥x轴,垂足为D,OB是△ACD的中位线.
的图象在第一象限交于点C,CD⊥x轴,垂足为D,OB是△ACD的中位线.
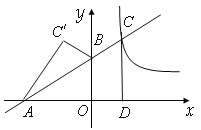
(1)求一次函数与反比例函数的解析式;
(2)若点C'是点C关于y轴的对称点,请求出△ABC'的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年9月17日世界人工智能大会在上海召开,人工智能的变革力在教育、制造等领域加速落地. 在某市举办的一次中学生机器人足球赛中,有四个代表队进入决赛,决赛中,每个队分别与其它三个队进行主客场比赛各一场(即每个队要进行6场比赛),以下是积分表的一部分.
排名 | 代表队 | 场次 (场) | 胜 (场) | 平 (场) | 负 (场) | 净胜球 (个) | 进球 (个) | 失球 (个) | 积分 (分) |
1 | A | 6 | 1 | 6 | 12 | 6 | 22 | ||
2 | B | 6 | 3 | 2 | 1 | 0 | 6 | 6 | 19 |
3 | C | 6 | 3 | 1 | 2 | 2 | 9 | 7 | 17 |
4 | D | 6 | 0 | 0 | 6 | m | 5 | 13 | 0 |
(说明:积分=胜场积分+平场积分+负场积分)
(1)D代表队的净胜球数m= ;
(2)本次决赛中,胜一场积 分,平一场积 分,负一场积 分;
(3)此次竞赛的奖金分配方案为:进入决赛的每支代表队都可以获得参赛奖金6000元;另外,在决赛期间,每胜一场可以再获得奖金2000元,每平一场再获得奖金1000元.
请根据表格提供的信息,求出冠军A队一共能获得多少奖金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平行四边形ABCD中,AE⊥BC,垂足为E,CE=AB,点F为CE的中点,点G在线段CD上,联结DF,交AG于点M,交EG于点N,且∠DFC=∠EGC.
(1)求证:CG=DG;
(2)求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】参照学习函数的过程方法,探究函数![]() 的图像与性质,因为
的图像与性质,因为![]() ,即
,即![]() ,所以我们对比函数
,所以我们对比函数![]() 来探究列表:
来探究列表:
| … | -4 | -3 | -2 | -1 |
|
| 1 | 2 | 3 | 4 | … | |
| … |
|
| 1 | 2 | 4 | -4 | -2 | -1 | <> |
| … | |
| … |
|
| 2 | 3 | 5 | -3 | -2 | 0 |
|
| … |
描点:在平面直角坐标系中以自变量![]() 的取值为横坐标,以
的取值为横坐标,以![]() 相应的函数值为纵坐标,描出相应的点如图所示:
相应的函数值为纵坐标,描出相应的点如图所示:
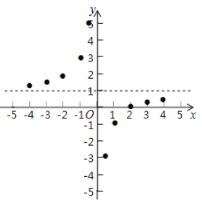
(1)请把![]() 轴左边各点和右边各点分别用一条光滑曲线,顺次连接起来;
轴左边各点和右边各点分别用一条光滑曲线,顺次连接起来;
(2)观察图象并分析表格,回答下列问题:
①当![]() 时,
时,![]() 随
随![]() 的增大而______;(“增大”或“减小”)
的增大而______;(“增大”或“减小”)
②![]() 的图象是由
的图象是由![]() 的图象向______平移______个单位而得到的;
的图象向______平移______个单位而得到的;
③图象关于点______中心对称.(填点的坐标)
(3)函数![]() 与直线
与直线![]() 交于点
交于点![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育老师统计了七年级甲、乙两个班女生的身高,并绘制了以下不完整的统计图.

请根据图中信息,解决下列问题:
(1)两个班共有女生多少人?
(2)将频数分布直方图补充完整;
(3)求扇形统计图中![]() 部分所对应的扇形圆心角度数;
部分所对应的扇形圆心角度数;
(4)身高在![]() 的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率.
的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com