
【题目】参照学习函数的过程方法,探究函数![]() 的图像与性质,因为
的图像与性质,因为![]() ,即
,即![]() ,所以我们对比函数
,所以我们对比函数![]() 来探究列表:
来探究列表:
| … | -4 | -3 | -2 | -1 |
|
| 1 | 2 | 3 | 4 | … | |
| … |
|
| 1 | 2 | 4 | -4 | -2 | -1 | <> |
| … | |
| … |
|
| 2 | 3 | 5 | -3 | -2 | 0 |
|
| … |
描点:在平面直角坐标系中以自变量![]() 的取值为横坐标,以
的取值为横坐标,以![]() 相应的函数值为纵坐标,描出相应的点如图所示:
相应的函数值为纵坐标,描出相应的点如图所示:
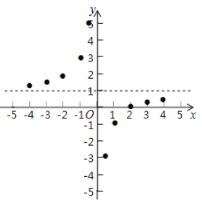
(1)请把![]() 轴左边各点和右边各点分别用一条光滑曲线,顺次连接起来;
轴左边各点和右边各点分别用一条光滑曲线,顺次连接起来;
(2)观察图象并分析表格,回答下列问题:
①当![]() 时,
时,![]() 随
随![]() 的增大而______;(“增大”或“减小”)
的增大而______;(“增大”或“减小”)
②![]() 的图象是由
的图象是由![]() 的图象向______平移______个单位而得到的;
的图象向______平移______个单位而得到的;
③图象关于点______中心对称.(填点的坐标)
(3)函数![]() 与直线
与直线![]() 交于点
交于点![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)如图所示,见解析;(2)①增大;②上,1;③![]() ;(3)1.
;(3)1.
【解析】
(1)按要求把![]() 轴左边点和右边各点分别用一条光滑曲线顺次连接起来即可;
轴左边点和右边各点分别用一条光滑曲线顺次连接起来即可;
(2)①观察图像可得出函数增减性;②由表格数据及图像可得出平移方式;③由图像可知对称中心;
(3)将![]() 与
与![]() 联立求解,得到A、B两点坐标,将△AOB分为△AOC与△BOC计算面积即可.
联立求解,得到A、B两点坐标,将△AOB分为△AOC与△BOC计算面积即可.
(1)如图所示:
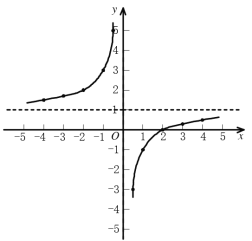
(2)①由图像可知:当![]() 时,
时,![]() 随
随![]() 的增大而增大,故答案为:增大;
的增大而增大,故答案为:增大;
②由表格数据及图像可知,![]() 的图象是由
的图象是由![]() 的图象向上平移1个单位而得到的,故答案为:上,1;
的图象向上平移1个单位而得到的,故答案为:上,1;
③由图像可知图像关于点(0,1)中心对称.
(3)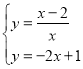 ,解得:
,解得:![]() 或
或![]()
∴A点坐标为(-1,3),B点坐标为(1,-1)
设直线![]() 与y轴交于点C,当x=0时,y=1,
与y轴交于点C,当x=0时,y=1,
所以C点坐标为(0,1),如图所示,
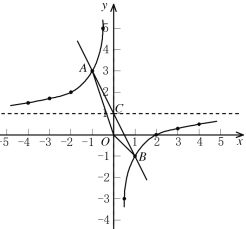
S△AOB= S△AOC+ S△BOC
=![]()
=![]()
=![]()
所以△AOB的面积为1.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小时,则∠AMN+∠ANM的度数是________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,y=ax2+bx-2的图象过A(1,0),B(-2,0),与y轴交于点C.
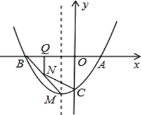
(1)求抛物线关系式及顶点M的坐标;
(2)若N为线段BM上一点,过N作x轴的垂线,垂足为Q,当N在线段BM上运动(N不与点B、点M重合),设NQ的长为t,四边形NQAC的面积为S,求S与t的关系式并求出S的最大值;
(3)在抛物线的对称轴上是否存在点P,使△PAC为直角三角形?若存在,请直接写出所有符合条件P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,AB=AC,求作△ABC的外心O,以下是甲、乙两同学的作法:
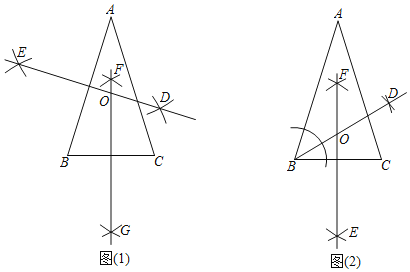
对于两人的作法:
甲:如图1,(1)作AB的垂直平分线DE;(2)作BC的垂直平分线FG;(3)DE,FG交于点O,则点O即为所求.
乙:如图2,(1)作∠ABC的平分线BD;(2)作BC的垂直平分线EF;(3)BD,EF交于点O,则点O即为所求.
对于两人的作法,正确的是( )
A.两人都对B.两人都不对C.甲对,乙不对D.甲不对,乙对
查看答案和解析>>
科目:初中数学 来源: 题型:
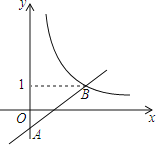
【题目】如图,在平面直角坐标系xOy中,一次函数y=ax﹣a(a为常数)的图象与y轴相交于点A,与函数![]() (x>0)的图象相交于点B(t,1).
(x>0)的图象相交于点B(t,1).
(1)求点B的坐标及一次函数的解析式;
(2)点P的坐标为(m,m)(m>0),过P作PE∥x轴,交直线AB于点E,作PF∥y轴,交函数![]() (x>0)的图象于点F.
(x>0)的图象于点F.
①若m=2,比较线段PE,PF的大小;
②直接写出使PE≤PF的m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高.某社区为了了解家庭对于文化教育的消费悄况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调査,根据调查结果绘制成两幅不完整的统计图表.
请你根据统计图表提供的信息,解答下列问题:
组別 | 家庭年文化教育消费金额x(元) | 户数 |
A | x≤5000 | 36 |
B | 5000<x≤10000 | m |
C | 10000<x≤15000 | 27 |
D | 15000<x≤20000 | 15 |
E | x>20000 | 30 |
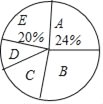
(1)本次被调査的家庭有__________户,表中 m=__________;
(2)本次调查数据的中位数出现在__________组.扇形统计图中,D组所在扇形的圆心角是__________度;
(3)这个社区有2500户家庭,请你估计家庭年文化教育消费10000元以上的家庭有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是甲、乙两个圆柱形水槽,一个圆柱形的空玻璃杯放置在乙槽中(空玻璃杯的厚度忽略不计).将甲槽的水匀速注入乙槽的空玻璃杯中,甲水槽内最高水位y(厘米)与注水时间t(分钟)之间的函数关系如图2线段DE所示,乙水槽(包括空玻璃杯)内最高水位y(厘米)与注水时间t(分钟)之间的函数关系如图2折线O﹣A﹣B﹣C所示.记甲槽底面积为S1,乙槽底面积为S2,乙槽中玻璃杯底面积为S3,则S1:S2:S3的值为_______.
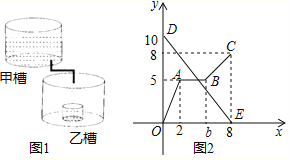
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李在景区销售一种旅游纪念品,已知每件进价为6元,当销售单价定为8元时,每天可以销售200件.市场调查反映:销售单价每提高1元,日销量将会减少10件,物价部门规定:销售单价不能超过12元,设该纪念品的销售单价为x(元),日销量为y(件),日销售利润为w(元).
(1)求y与x的函数关系式.
(2)要使日销售利润为720元,销售单价应定为多少元?
(3)求日销售利润w(元)与销售单价x(元)的函数关系式,当x为何值时,日销售利润最大,并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com