
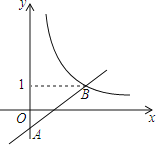
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌвЛДЮКЏЪ§yЃНaxЉaЃЈaЮЊГЃЪ§ЃЉЕФЭМЯѓгыyжсЯрНЛгкЕуAЃЌгыКЏЪ§![]() ЃЈxЃО0ЃЉЕФЭМЯѓЯрНЛгкЕуBЃЈtЃЌ1ЃЉЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓЯрНЛгкЕуBЃЈtЃЌ1ЃЉЃЎ
ЃЈ1ЃЉЧѓЕуBЕФзјБъМАвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
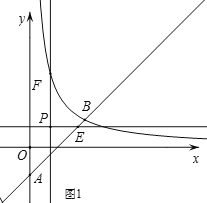
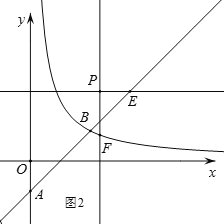
ЃЈ2ЃЉЕуPЕФзјБъЮЊЃЈmЃЌmЃЉЃЈmЃО0ЃЉЃЌЙ§PзїPEЁЮxжсЃЌНЛжБЯпABгкЕуEЃЌзїPFЁЮyжсЃЌНЛКЏЪ§![]() ЃЈxЃО0ЃЉЕФЭМЯѓгкЕуFЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓгкЕуFЃЎ
ЂйШєmЃН2ЃЌБШНЯЯпЖЮPEЃЌPFЕФДѓаЁЃЛ
ЂкжБНгаДГіЪЙPEЁмPFЕФmЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНxЉ1ЃЛЃЈ2ЃЉЂйPEЃНPFЃЛЂк0ЃМmЁм1ЛђmЁн2ЃЎ
ЁОНтЮіЁП
(1)АбB(tЃЌ1)ДњШыЗДБШР§КЏЪ§НтЮіЪНМДПЩЧѓЕУBЕФзјБъЃЌНјЖјАбBЕФзјБъДњШыyЃНaxЉaИљОнД§ЖЈЯЕЪ§ЗЈМДПЩЧѓЕУвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
(2)ЂйвРОнPEЁЮxжсЃЌНЛжБЯпABгкЕуEЃЌPFЁЮyжсЃЌНЛКЏЪ§![]() (xЃО0)ЕФЭМЯѓгкЕуFЃЌМДПЩЕУЕНPEЃНPFЃЛЂкЕБmЃН2ЃЌPEЃНPFЃЛЕБmЃН1ЃЌPEЃНPFЃЛвРОнPEЁмPFЃЌМДПЩгЩЭМЯѓЕУЕН0ЃМmЁм1ЛђmЁн2ЃЎ
(xЃО0)ЕФЭМЯѓгкЕуFЃЌМДПЩЕУЕНPEЃНPFЃЛЂкЕБmЃН2ЃЌPEЃНPFЃЛЕБmЃН1ЃЌPEЃНPFЃЛвРОнPEЁмPFЃЌМДПЩгЩЭМЯѓЕУЕН0ЃМmЁм1ЛђmЁн2ЃЎ
(1)ЁпКЏЪ§![]() (xЃО0)ЕФЭМЯѓОЙ§ЕуB(tЃЌ1)ЃЌ
(xЃО0)ЕФЭМЯѓОЙ§ЕуB(tЃЌ1)ЃЌ
ЁрtЃН2ЃЌ
ЁрB(2ЃЌ1)ЃЌ
ДњШыyЃНaxЉaЕУЃЌ1ЃН2aЉaЃЌ
ЁрaЃН1ЃЌ
ЁрвЛДЮКЏЪ§ЕФНтЮіЪНЮЊyЃНxЉ1ЃЛ
(2)ЂйЕБmЃН2ЪБЃЌЕуPЕФзјБъЮЊ(2ЃЌ2)ЃЌ
гжЁпPEЁЮxжсЃЌНЛжБЯпABгкЕуEЃЌPFЁЮyжсЃЌНЛКЏЪ§![]() (xЃО0)ЕФЭМЯѓгкЕуFЃЌ
(xЃО0)ЕФЭМЯѓгкЕуFЃЌ
ЁрЕБyЃН2ЪБЃЌ2ЃНxЉ1ЃЌМДxЃН3ЃЌ
ЁрPEЃН3Љ2ЃН1ЃЌ
ЕБxЃН2ЪБЃЌ![]() ЃН1ЃЌ
ЃН1ЃЌ
ЁрPFЃН2Љ1ЃН1ЃЌ
ЁрPEЃНPFЃЛ

ЂкгЩЂйПЩЕУЃЌЕБmЃН2ЃЌPEЃНPFЃЛ
ЁпPEЃНm+1ЉmЃН1ЃЌ
Сю![]() ЉmЃН1ЃЌдђmЃН1ЛђmЃНЉ2(ЩсШЅ)ЃЌ
ЉmЃН1ЃЌдђmЃН1ЛђmЃНЉ2(ЩсШЅ)ЃЌ
ЁрЕБmЃН1ЃЌPEЃНPFЃЛ
ЁпPEЁмPFЃЌ
ЁргЩЭМЯѓПЩЕУЃЌ0ЃМmЁм1ЛђmЁн2ЃЎ


 ЕМбЇШЋГЬСЗДДгХбЕСЗЯЕСаД№АИ
ЕМбЇШЋГЬСЗДДгХбЕСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌABЃНACЃЌЁЯBACЃН90ЁуЃЌжБНЧЁЯEPFЕФЖЅЕуPЪЧBCЕФжаЕуЃЌСНБпPEЃЌPFЗжБ№НЛABЃЌACгкЕуEЃЌFЃЌЯжИјГівдЯТЫФИіНсТлЃКЃЈ1ЃЉAEЃНCFЃЛЃЈ2ЃЉЁїEPFЪЧЕШбќжБНЧШ§НЧаЮЃЛЃЈ3ЃЉSЫФБпаЮAEPFЃН![]() SЁїABCЃЛЃЈ4ЃЉЕБЁЯEPFдкЁїABCФкШЦЖЅЕуPа§зЊЪБЪМжегаEFЃНAPЃЎЃЈЕуEВЛгыAЁЂBжиКЯЃЉЃЌЩЯЪіНсТлжаЪЧе§ШЗЕФНсТлЕФИХТЪЪЧЃЈЁЁЁЁЃЉ
SЁїABCЃЛЃЈ4ЃЉЕБЁЯEPFдкЁїABCФкШЦЖЅЕуPа§зЊЪБЪМжегаEFЃНAPЃЎЃЈЕуEВЛгыAЁЂBжиКЯЃЉЃЌЩЯЪіНсТлжаЪЧе§ШЗЕФНсТлЕФИХТЪЪЧЃЈЁЁЁЁЃЉ

A.1ИіB.3ИіC.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжБЯпyЃНk1xЃЋbНЛxжсгкЕуAЃЈЃ3ЃЌ0ЃЉЃЌНЛyжсгкЕуBЃЈ0ЃЌ2ЃЉЃЌВЂгы![]() ЕФЭМЯѓдкЕквЛЯѓЯоНЛгкЕуCЃЌCDЁЭxжсЃЌДЙзуЮЊDЃЌOBЪЧЁїACDЕФжаЮЛЯпЃЎ
ЕФЭМЯѓдкЕквЛЯѓЯоНЛгкЕуCЃЌCDЁЭxжсЃЌДЙзуЮЊDЃЌOBЪЧЁїACDЕФжаЮЛЯпЃЎ
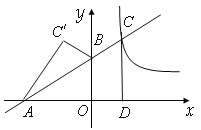
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§гыЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуC'ЪЧЕуCЙигкyжсЕФЖдГЦЕуЃЌЧыЧѓГіЁїABC'ЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊдкЦНааЫФБпаЮABCDжаЃЌAEЁЭBCЃЌДЙзуЮЊEЃЌCE=ABЃЌЕуFЮЊCEЕФжаЕуЃЌЕуGдкЯпЖЮCDЩЯЃЌСЊНсDFЃЌНЛAGгкЕуMЃЌНЛEGгкЕуNЃЌЧвЁЯDFC=ЁЯEGCЃЎ
ЃЈ1ЃЉЧѓжЄЃКCG=DGЃЛ
ЃЈ2ЃЉЧѓжЄЃК![]() ЃЎ
ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
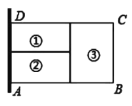
ЁОЬтФПЁПЮЊСЫНкЪЁВФСЯЃЌФГХЉГЁжїРћгУЮЇЧНЃЈЮЇЧНзуЙЛГЄЃЉЮЊвЛБпЃЌгУзмГЄЮЊ![]() ЕФРщАЪЮЇГЩСЫШчЭМЫљЪОЕФЂйЂкЂлШ§ПщОиаЮЧјгђЃЌЖјЧветШ§ПщОиаЮЧјгђЕФУцЛ§ЯрЕШЃЌдђ
ЕФРщАЪЮЇГЩСЫШчЭМЫљЪОЕФЂйЂкЂлШ§ПщОиаЮЧјгђЃЌЖјЧветШ§ПщОиаЮЧјгђЕФУцЛ§ЯрЕШЃЌдђ![]() ГЄЮЊ______ЪБЃЌФмЮЇГЩЕФОиаЮЧјгђ
ГЄЮЊ______ЪБЃЌФмЮЇГЩЕФОиаЮЧјгђ![]() ЕФУцЛ§зюДѓЃЎ
ЕФУцЛ§зюДѓЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПВЮеебЇЯАКЏЪ§ЕФЙ§ГЬЗНЗЈЃЌЬНОПКЏЪ§![]() ЕФЭМЯёгыаджЪЃЌвђЮЊ
ЕФЭМЯёгыаджЪЃЌвђЮЊ![]() ЃЌМД
ЃЌМД![]() ЃЌЫљвдЮвУЧЖдБШКЏЪ§
ЃЌЫљвдЮвУЧЖдБШКЏЪ§![]() РДЬНОПСаБэЃК
РДЬНОПСаБэЃК
| Ё | -4 | -3 | -2 | -1 |
|
| 1 | 2 | 3 | 4 | Ё | |
| Ё |
|
| 1 | 2 | 4 | -4 | -2 | -1 | <> |
| Ё | |
| Ё |
|
| 2 | 3 | 5 | -3 | -2 | 0 |
|
| Ё |
УшЕуЃКдкЦНУцжБНЧзјБъЯЕжавдздБфСП![]() ЕФШЁжЕЮЊКсзјБъЃЌвд
ЕФШЁжЕЮЊКсзјБъЃЌвд![]() ЯргІЕФКЏЪ§жЕЮЊзнзјБъЃЌУшГіЯргІЕФЕуШчЭМЫљЪОЃК
ЯргІЕФКЏЪ§жЕЮЊзнзјБъЃЌУшГіЯргІЕФЕуШчЭМЫљЪОЃК
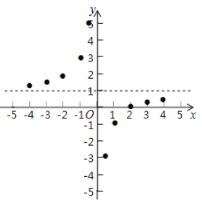
ЃЈ1ЃЉЧыАб![]() жсзѓБпИїЕуКЭгвБпИїЕуЗжБ№гУвЛЬѕЙтЛЌЧњЯпЃЌЫГДЮСЌНгЦ№РДЃЛ
жсзѓБпИїЕуКЭгвБпИїЕуЗжБ№гУвЛЬѕЙтЛЌЧњЯпЃЌЫГДЮСЌНгЦ№РДЃЛ
ЃЈ2ЃЉЙлВьЭМЯѓВЂЗжЮіБэИёЃЌЛиД№ЯТСаЮЪЬтЃК
ЂйЕБ![]() ЪБЃЌ
ЪБЃЌ![]() Ыц
Ыц![]() ЕФдіДѓЖј______ЃЛЃЈЁАдіДѓЁБЛђЁАМѕаЁЁБЃЉ
ЕФдіДѓЖј______ЃЛЃЈЁАдіДѓЁБЛђЁАМѕаЁЁБЃЉ
Ђк![]() ЕФЭМЯѓЪЧгЩ
ЕФЭМЯѓЪЧгЩ![]() ЕФЭМЯѓЯђ______ЦНвЦ______ИіЕЅЮЛЖјЕУЕНЕФЃЛ
ЕФЭМЯѓЯђ______ЦНвЦ______ИіЕЅЮЛЖјЕУЕНЕФЃЛ
ЂлЭМЯѓЙигкЕу______жааФЖдГЦ.ЃЈЬюЕуЕФзјБъЃЉ
ЃЈ3ЃЉКЏЪ§![]() гыжБЯп
гыжБЯп![]() НЛгкЕу
НЛгкЕу![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФУцЛ§.
ЕФУцЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
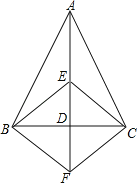
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкЁїABCжаЃЌABЃНACЃЌADЪЧBCБпЩЯЕФжаЯпЃЌЕуEЪЧADЩЯвЛЕуЃЌЙ§ЕуBзїBFЁЮECЃЌНЛADЕФбгГЄЯпгкЕуFЃЌСЌНгBEЃЌCFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїBDFЁеЁїCDEЃЛ
ЃЈ2ЃЉЕБEDгыBCТњзуЪВУДЪ§СПЙиЯЕЪБЃЌЫФБпаЮBECFЪЧе§ЗНаЮЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
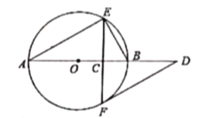
ЁОЬтФПЁПШчЭМЃЌ![]() ЪЧ
ЪЧ![]() ЕФжБОЖЃЌЯв
ЕФжБОЖЃЌЯв![]() гкЕу
гкЕу![]() ЃЛЕу
ЃЛЕу![]() ЪЧ
ЪЧ![]() бгГЄЯпЩЯвЛЕуЃЌ
бгГЄЯпЩЯвЛЕуЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЪЧ
ЪЧ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
ЃЈ2ЃЉШЁ![]() ЕФжаЕу
ЕФжаЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌШє
ЃЌШє![]() ЕФАыОЖЮЊ2ЃЌЧѓ
ЕФАыОЖЮЊ2ЃЌЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
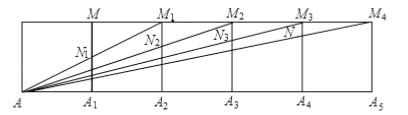
ЁОЬтФПЁПНЋ2019ИіБпГЄЮЊlЕФе§ЗНаЮАДШчЭМЫљЪОЕФЗНЪНХХСаЃЌЕу![]() КЭЕу
КЭЕу![]() ЪЧе§ЗНаЮЕФЖЅЕуЃЌСЌНг
ЪЧе§ЗНаЮЕФЖЅЕуЃЌСЌНг![]() ЗжБ№НЛе§ЗНаЮЕФБп
ЗжБ№НЛе§ЗНаЮЕФБп![]() гкЕу
гкЕу![]() ЃЌЫФБпаЮ
ЃЌЫФБпаЮ![]() ЕФУцЛ§ЪЧ
ЕФУцЛ§ЪЧ![]() ЃЌЫФБпаЮ
ЃЌЫФБпаЮ![]() ЕФУцЛ§ЪЧ
ЕФУцЛ§ЪЧ![]() ЃЌЁЃЌдђ
ЃЌЁЃЌдђ![]() ЮЊ_________ЃЎ
ЮЊ_________ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com