【题目】在平面直角坐标系中，我们把横、纵坐标均为整数的点叫做整点，已知反比例函数y＝
（m＜0）与y＝x2﹣5在第四象限内围成的封闭图形（包括边界）内的整点的个数为4，则实数m的取值范围为_____．
中考解读考点精练系列答案科目：初中数学 来源： 题型：
【题目】为了增强学生的疫情防控意识，响应“停课不停学”号召，某校组织了一次“疫情防控知识”专题网上学习，并进行了一次全校2500名学生都参加的网上测试．阅卷后，教务处随机抽取了100份答卷进行分析统计，发现考试成绩（
分）的最低分为51分，最高分为满分100分，并绘制了如下不完整的统计图表．请根据图表提供的信息，解答下列问题：
分数段（分） | 频数（人） | 频率 |
|
| 0.1 |
| 18 | 0.18 |
|
|
|
| 35 | 0.35 |
| 12 | 0.12 |
合计 | 100 | 1 |
（1）填空：
________，
________，
________；
（2）将频数分布直方图补充完整；
（3）该校对成绩为
的学生进行奖励，按成绩从高分到低分设一、二、三等奖，并且一、二、三等奖的人数比例为
，请你估算全校获得二等奖的学生人数；
（4）结合调查的情况，为了提高疫情防控意识，请你给学校提一条合理性建议．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，y=ax2+bx－2的图象过A（1，0），B（－2，0），与y轴交于点C．
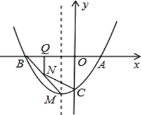
（1）求抛物线关系式及顶点M的坐标；
（2）若N为线段BM上一点，过N作x轴的垂线，垂足为Q，当N在线段BM上运动（N不与点B、点M重合），设NQ的长为t，四边形NQAC的面积为S，求S与t的关系式并求出S的最大值；
（3）在抛物线的对称轴上是否存在点P，使△PAC为直角三角形？若存在，请直接写出所有符合条件P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，E、F分别是平行四边形ABCD的边AD、BC上的点，且BE∥DF，AC分别交BE、DF于点G、H．下列结论：①四边形BFDE是平行四边形；②△AGE≌△CHF；③BG=DH；④S△AGE：S△CDH=GE：DH，其中正确的个数是( )
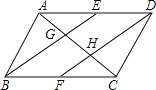
A.1B.2个C.3个D.4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，直线y＝kx（k≠0）与双曲线y＝
（x＞0）交于点A（2，n）．
（1）求n及k的值；
（2）点B是y轴正半轴上的一点，且△OAB是等腰三角形，请直接写出所有符合条件的点B的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
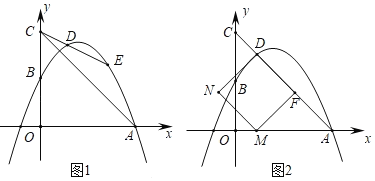
【题目】如图1，二次函数y
x2+bx+c的图象过A(5，0)和B(0，
)两点，射线CE绕点C(0，5)旋转，交抛物线于D，E两点，连接AC．
（1）求二次函数yx2+bx+c的表达式；
（2）连接OE，AE，当△CEO是以CO为底的等腰三角形时，求点E的坐标和△ACE的面积；
（3）如图2，射线CE旋转时，取DE的中点F，以DF为边作正方形DFMN．当点E和点A重合时，正方形DFMN的顶点M恰好落在x轴上．
①求点M的坐标；
②当点E和点A重合时，将正方形DFMN沿射线CE方向以每秒
个单位长度平移．设运动时间为t秒．直接写出正方形DFMN落在x轴下方的面积S与时间t(0≤t≤4)的函数表达式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】数学学习小组根据函数学习的经验，对一个新函数
的图象和性质进行了如下探究：
列表，下表是函数
与自变量
的几组对应值
| ··· |
|
|
|
|
|
|
|
|
|
| ··· |
| ··· |
|
|
|
|
|
|
|
|
|
| ··· |
请直接写出
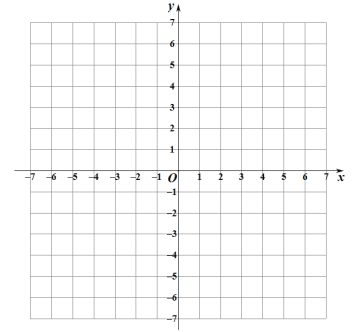
如图，在平面直角系
中，描出上表中各对对应值为坐标的点 （其中为横坐标，为纵坐标），并根据描出的点画出函数的图象
观察所画出的函数图象，写出该函数的性质（写一条性质即可）
请结合画出的函数图象与表格中数据，直接写出关于的不等式的解集：
查看答案和解析>>
科目：初中数学 来源： 题型：
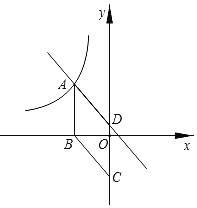
【题目】如图，在直角坐标系中，菱形ABCD的边长为5，面积为15，点A在双曲线y＝
上，点B在x轴上，C、D在y轴上．
（1）求顶点A的坐标和k的值．
（2）求直线AD的解析式．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
